Question

【题目】设方程（m+1）|ex﹣1|﹣1=0的两根分别为x1 ， x2（x1＜x2），方程|ex﹣1|﹣m=0的两根分别为x3 ， x4（x3＜x4）．若m∈（0， ），则（x4+x1）﹣（x3+x2）的取值范围为（ ）
A.（﹣∞，0）
B.（﹣∞，ln ）
C.（ln ，0）
D.（﹣∞，﹣1）

Answer 1

【答案】B
【解析】解：由方程（m+1）|ex﹣1|﹣1=0的两根为x1 ， x2（x1＜x2），可得 ， ， 求得x1=ln ，x2=ln ．
由方程|ex﹣1|﹣m=0的两根为x3 ， x4（x3＜x4），可得 ，
求得x3=ln（1﹣m），x4=ln（1+m）．
∴（x4+x1）﹣（x3+x2）=lnm﹣ln =ln ．
令t= ，则原式=lnt，且 ．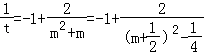
由m∈（0， ），可得 0＜ ＜ ， ，
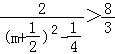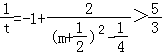∴ ，则0 ．
故原式=lnt∈（﹣∞，ln ），
故选：B．
由条件求得x1 ， x2 ， x3 ， x4 ， 得到（x4+x1）﹣（x3+x2）=ln ．令t= ，则原式=lnt，利用不等式的基本性质求得 的范围，可得t的范围，
从而求得lnt的范围，即为所求．