题目内容
【题目】已知函数![]() 的图像与
的图像与![]() 轴的相邻两交点的坐标分别为
轴的相邻两交点的坐标分别为![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() 有最小值.
有最小值.
(1)求函数![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)将![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像的横坐标伸长为原来的
个单位,再将所得图像的横坐标伸长为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图像,若关于
的图像,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个解,求
上有两个解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]()
![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由题意可知![]() ,可求得
,可求得![]() ,又
,又![]() ,可求
,可求![]() ,可得
,可得![]() ,再根据余弦函数的单调性,即可求出函数
,再根据余弦函数的单调性,即可求出函数![]() 的单调递减区间;
的单调递减区间;
(2)根据图像平移可得,函数![]() ,因为
,因为![]() 在
在![]() 上有两个解,所以
上有两个解,所以![]() 与
与![]() 在
在![]() 上有两个交点,据此列出不等式,即可求出结果.
上有两个交点,据此列出不等式,即可求出结果.
(1)由题得![]() ,∴
,∴![]() .
.
所以![]() ,∵
,∵![]() ,
,
又![]() ,∴
,∴![]() .
.
所以![]() .
.
令![]() ,∴
,∴![]() ,
,![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .
.
(2)将![]() 的图像向右平移
的图像向右平移![]() 个单位得到
个单位得到![]() ,再将横坐标伸长为原来的
,再将横坐标伸长为原来的![]() 倍,得到函数
倍,得到函数![]() ,
,
因为![]() 在
在![]() 上有两个解,所以
上有两个解,所以![]() 与
与![]() 在
在![]() 上有两个交点,
上有两个交点,
因为![]() ,所以
,所以![]() 或
或![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).

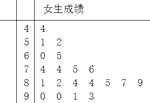
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间![]() 与每天获得的利润
与每天获得的利润![]() (单位:万元)的有关数据.
(单位:万元)的有关数据.
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)估计星期日获得的利润为多少万元.
参考公式: 
【题目】某种工业机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:
方案一:交纳延保金700元,在延保的两年内可免费维修2次,超过2次每次收取维修费200元;
方案二:交纳延保金1000元,在延保的两年内可免费维修4次,超过4次每次收取维修费100元.
某工厂准备一次性购买2台这种机器.现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 20 | 10 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率.记X表示这2台机器超过质保期后延保的两年内共需维修的次数.
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,工厂选择哪种延保方案更合算?