Question

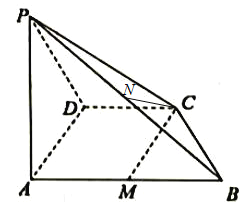
【题目】如图，已知矩形ABCD中，，，M是以CD为直径的半圆周上的任意一点（与C，D均不重合），且平面平面ABCD.

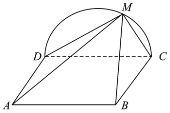
（1）求证：平面平面BCM；

（2）当四棱锥的体积最大时，求AM与CD所成的角.

Answer 1

【答案】（1）证明见解析 （2）

【解析】

（1）只证明CM⊥平面ADM即可，即证明CM垂直于该平面内的两条相交直线，或者使用面面垂直的性质，本题的条件是平面CDM⊥平面ABCD，而M是以CD为直径的半圆周上一点，能够得到CM⊥DM，由面面垂直的性质即可证明；（2）当四棱锥M一ABCD的体积最大时，M为半圆周中点处，可得角MAB就是AM与CD所成的角，利用已知即可求解．

（1）证明：CD为直径，所以CMDM ，

已知平面CDM平面ABCD， ADCD，

AD平面CDM，所以ADCM 又DMAD=D

CM平面ADM 又CM平面BCM，

平面ADM平面BCM ，

（2）

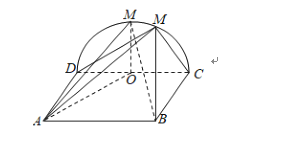
当M为半圆弧CD的中点时，四棱锥的体积最大，

此时，过点M作MOCD于点E,

平面CDM平面ABCD

MO平面ABCD，即MO为四棱锥的高又底面ABCD面积为定值2，

AM与CD所成的角即AM与AB所成的角，

求得为正三角形，

，故AM与CD所成的角为