题目内容
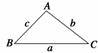
如图所示，在△ABC中，射影定理可表示为a＝b·cos C＋c·cos B，其
中a，b，c分别为角A，B，C的对边，类比上述定理，写出对空间
四面体性质的猜想．
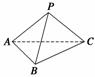解 如图所示，在四面体P－ABC中，设S1，S2，S3，S分别表示△PAB，
△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，
面PCA与底面ABC所成二面角的大小．
我们猜想射影定理类比推理到三维空间，其表现形式应为：S＝S1·cos α＋S2·cos β＋S3·cos γ.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图所示，在△ABC，已知
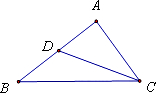如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
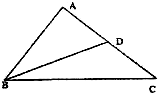如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=
如图所示，在△ABC中，∠BAC=90°，∠ABC=60°，AD⊥BC于D，则
如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=