题目内容
已知sin(α-
)=
,则cos(α+
)=( )
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:运用-α、
-α的诱导公式,计算即可得到.
| π |
| 2 |
解答:
解:sin(α-
)=
,即为
sin(
-α)=-
,
即有sin[
-(
+α)]=-
,
即cos(α+
)=-
.
故选A.
| π |
| 4 |
| 1 |
| 3 |
sin(
| π |
| 4 |
| 1 |
| 3 |
即有sin[
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
即cos(α+
| π |
| 4 |
| 1 |
| 3 |
故选A.
点评:本题考查三角函数的求值,考查三角函数的诱导公式的运用,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
sin15°cos15°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
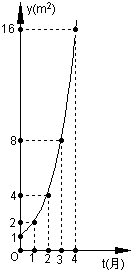 如图是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at的图象,有以下叙述,其中正确的是( )
如图是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at的图象,有以下叙述,其中正确的是( )①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30m2;
③浮萍每月增加的面积都相等;
④若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.
| A、①② | B、①②③④ |
| C、②③④ | D、①②④ |
已知圆的方程为x2+y2-6x-8y=0,设该圆过点(3,7)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
| A、10 | B、20 | C、30 | D、40 |
命题p:?a∈R,使得x2+ax+1=0有解,则?p为( )
| A、?a∈R,使得x2+ax+1≠0有解 |
| B、?a∈R,使得x2+ax+1=0无解 |
| C、?a∈R,都有x2+ax+1=0无解 |
| D、?a∈R,都有x2+ax+1≠0无解 |
数列{an}的通项公式an=
,则S5=( )
| 1 |
| n(n+1) |
| A、1 | ||
B、
| ||
C、
| ||
D、
|