题目内容
已知函数
在
处取得极值.
（Ⅰ）求函数
的单调区间；
（Ⅱ）求证：
，
．
（1）函数
的单调增区间为
，
，单调减区间为
.
（2）见解析
解析:
（Ⅰ）
由
得 
…………………………4分
，
|
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
| 极大值 |
| 极小值 |
|
故函数的单调增区间为，，单调减区间为.
……………………………………8分
（Ⅱ）由（Ⅰ）在递增，在递减，
递增，在
时取极大值
又
. 
∴在
上，
.
又
故
（当且仅当
时取等号）.
即
的最小值为
.
，
．……………………12分
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
在
处取得极值.
；
，如果
在开区间
上存在极小值，求实数
的取值范围.
=
在
处取得极值.
的值；
的方程
在
上恰有两个不相等的实数根，求实数
的取值范围；
在
处取得极值。
的解析式；
上任意两个自变量的值
，都有
；
可作曲线
的三条切线，求实数
的取值范围。
为实数。
在
处取得极值，求
的值；
对任意
都成立，求实数
的取值范围。
在
处取得极值．
的值；[来源:学+科+网]
的方程
在区间
上恰有两个不同的实数根，求实数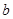
的取值范围．