题目内容
甲商店某种商品11月份(30天,11月1日为第一天)的销售价格P(元)与时间t(天)函数关系如图(一)所示,该商品日销售量Q(件)与时间t(天)函数关系如图(二)所示.
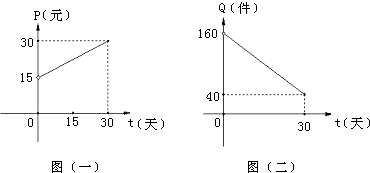
(1)写出图(一)表示的销售价格与时间的函数关系式P=f(t)及其定义域,写出图(二)表示的日销售量与时间的函数关系式Q=g(t)及其定义域;
(2)写出日销售金额M(元)与时间t的函数关系式M=h(t)及其定义域并求M的最大值.(注:日销售金额M=销售价格P×日销售量Q).

(1)写出图(一)表示的销售价格与时间的函数关系式P=f(t)及其定义域,写出图(二)表示的日销售量与时间的函数关系式Q=g(t)及其定义域;
(2)写出日销售金额M(元)与时间t的函数关系式M=h(t)及其定义域并求M的最大值.(注:日销售金额M=销售价格P×日销售量Q).
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(1)设价格函数是y=kt+b,且过点(0,15)、(30,30),代入可求得f(t);同理,可求得销售量函数g(t);
(2)日销售金额与时间的函数M=h(t)=f(t)•g(t),再求最值即可.
(2)日销售金额与时间的函数M=h(t)=f(t)•g(t),再求最值即可.
解答:
解:(1)设价格函数是y=kt+b,过点(0,15)、(30,30),则
,
∴b=15,k=
;
∴ff(t)=
t+15(0<t≤30,t∈N);
设销售量函数y=at+m,过点(0,160),(30,40),
则
,∴m=160,a=-4;
∴g(t)=-4t+160(0<t≤30)(t∈N);
(2)M=h(t)=(
t+15)(-4t+160)=-2t2+20t+2400(0<t≤30,t∈N)
∴t=5时,M的最大值为2450元.
|
∴b=15,k=
| 1 |
| 2 |
∴ff(t)=
| 1 |
| 2 |
设销售量函数y=at+m,过点(0,160),(30,40),
则
|
∴g(t)=-4t+160(0<t≤30)(t∈N);
(2)M=h(t)=(
| 1 |
| 2 |
∴t=5时,M的最大值为2450元.
点评:本题由图象考查了一次函数的解析式,以及二次函数的最值,是中档题目.

练习册系列答案
相关题目
在钝角△ABC中,a=1,b=2,则最大边c的取值范围是( )
| A、1<c<3 | ||
| B、2<c<3 | ||
C、
| ||
D、2
|