题目内容
(本小题满分14分)已知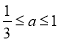 , 若函数
, 若函数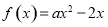 在
在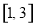 上的最大值为
上的最大值为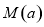 ,最小值为
,最小值为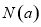 , 令
, 令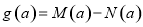 .
.
(1)求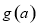 的表达式;
的表达式;
(2)若关于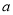 的方程
的方程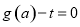 有解,求实数
有解,求实数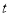 的取值范围.
的取值范围.
(1)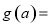
 ;(2)实数
;(2)实数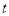 的取值范围为
的取值范围为 .
.
【解析】
试题分析:(1)这是区间定轴变的二次函数的最值题型,所给二次函数的对称轴为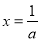 ,根据
,根据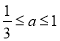 ,可知对称轴
,可知对称轴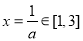 ,因为即涉及二次函数的最大值与最小值,故分
,因为即涉及二次函数的最大值与最小值,故分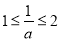 ,
,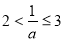 两种情况进行讨论,结合二次函数的图像确定最值,进而可求出
两种情况进行讨论,结合二次函数的图像确定最值,进而可求出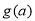 的表达式;(2)根据(1)中确定的
的表达式;(2)根据(1)中确定的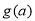 的表达式,先用证明函数单调性的方法证明函数
的表达式,先用证明函数单调性的方法证明函数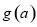 在
在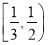 上单调递减,在
上单调递减,在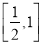 上单调递增,进而确定函数
上单调递增,进而确定函数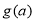 的值域,而关于
的值域,而关于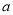 的方程
的方程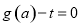 有解等价于
有解等价于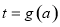 有解,即
有解,即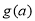 在
在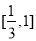 的值域就是
的值域就是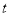 的取值范围,问题得以解决.
的取值范围,问题得以解决.
试题解析:(1)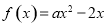
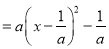 1分
1分
∵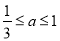 ,∴
,∴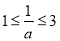
①当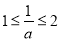 ,即
,即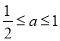 时,则
时,则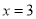 时,函数
时,函数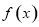 取得最大值;
取得最大值;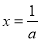 时,函数
时,函数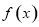 取得最小值.
取得最小值.
∴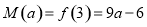 ,
,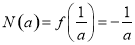
∴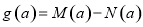
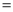
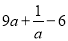 3分
3分
②当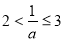 ,即
,即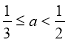 时,则
时,则 时,函数
时,函数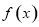 取得最大值;
取得最大值;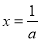 时,函数
时,函数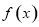 取得最小值.
取得最小值.
∴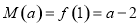 ,
,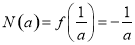
∴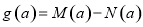
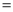
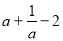 . 5分
. 5分
综上,得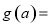
 6分
6分
(2)任取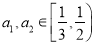 ,且
,且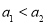
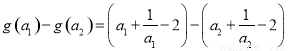
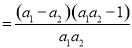 7分
7分
∵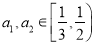 ,且
,且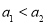
∴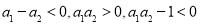
∴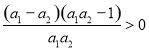 ,即
,即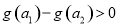
∴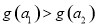
∴函数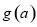 在
在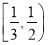 上单调递减 8分
上单调递减 8分
任取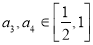 ,且
,且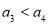
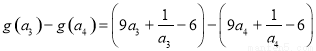
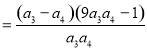 9分
9分
∵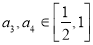 ,且
,且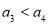
∴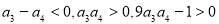
∴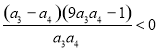 ,即
,即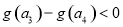
∴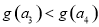
∴函数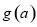 在
在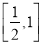 上单调递增 10分
上单调递增 10分
当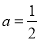 时,
时,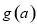 取得最小值,其值为
取得最小值,其值为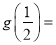
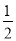 11分
11分
又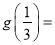
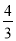 ,
,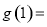
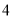
∴函数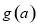 的值域为
的值域为 12分
12分
∵关于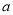 的方程
的方程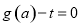 有解等价于
有解等价于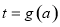 有解
有解
∴实数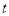 的取值范围为函数
的取值范围为函数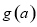 的值域 13分
的值域 13分
∴实数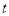 的取值范围为
的取值范围为 14分.
14分.
考点:1.二次函数的图像与性质;2.函数与方程;3.分类讨论的思想.

练习册系列答案
相关题目
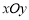 中,已知曲线
中,已知曲线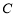 的参数方程是
的参数方程是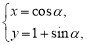 (
(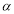 是参数),若以
是参数),若以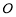 为极点,
为极点,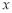 轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线
轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线 的极坐标方程.
的极坐标方程. 中,
中, ,则
,则 ( )
( )
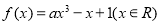 ,若对于任意
,若对于任意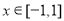 都有
都有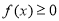 ,则实数a的取值范围为( )
,则实数a的取值范围为( )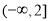 B.
B.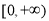 C.
C.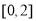 D.
D.
 是等比数列
是等比数列 的前n项和,若
的前n项和,若 ,则
,则 ( )
( ) C.
C. D.1或2
D.1或2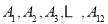 的
的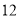 名篮球运动员在某次篮球比赛中的得分记录如下:
名篮球运动员在某次篮球比赛中的得分记录如下:






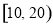 内的运动员中随机抽取
内的运动员中随机抽取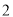 人 , 求这
人 , 求这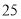 的概率.
的概率.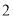 的等腰梯形,则该几何体的体积为( )
的等腰梯形,则该几何体的体积为( )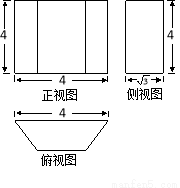
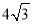 B.
B.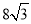 C.
C.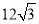 D.
D.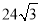
 ,则
,则 是直角三角形”的否命题的真假性为
是直角三角形”的否命题的真假性为  满足
满足 ,
, ,
, ,
, ,则
,则 的最小值为 .
的最小值为 .