题目内容
椭圆 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为 ,点M是椭圆C上一点,
,点M是椭圆C上一点, 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为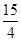 .
.
(1)求椭圆C以及圆O的方程;
(2)当点 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线 与圆O的位置关系.
与圆O的位置关系.
(1) ,
,
(2)直线l与圆O相交.
解析试题分析:解:(1)设椭圆C的半焦距为c,则 ,即
,即 ① 1分
① 1分
又 ② 3分
② 3分
联立①②,解得 ,所以
,所以 .
.
所以椭圆C的方程为 . 5分
. 5分
而椭圆C上点 与椭圆中心O的距离为
与椭圆中心O的距离为 ,等号在
,等号在 时成立 7分,
时成立 7分,
而 ,则
,则 的最小值为
的最小值为 ,从而
,从而 ,则圆O的方程为
,则圆O的方程为 . 9分
. 9分
(2)因为点 在椭圆C上运动,所以
在椭圆C上运动,所以 .即
.即 .
.
圆心O到直线 的距离
的距离 . 12分
. 12分
当 ,
, ,则直线l与圆O相交. 14分
,则直线l与圆O相交. 14分
考点:椭圆方程和圆的方程
点评:主要是考查了椭圆的方程以及直线与圆的位置关系的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 离心率为
离心率为 直线
直线 与C的两个交点间的距离为
与C的两个交点间的距离为
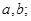 ;
; 的直线l与C的左、右两支分别相交有A、B两点,且
的直线l与C的左、右两支分别相交有A、B两点,且 证明:
证明:
 的离心率为
的离心率为 ,椭圆与x轴交于两点
,椭圆与x轴交于两点 、
、 ,过点C的直线
,过点C的直线 与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
 为定值.
为定值.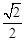 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线:x=-
(a>b>0)的左、右焦点,直线:x=-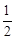 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.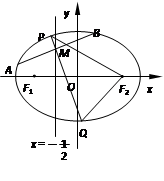
 的取值范围.
的取值范围. :
: 的离心率为
的离心率为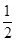 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值.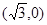
 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围. 的左顶点为
的左顶点为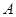 ,
, 是椭圆
是椭圆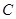 上异于点
上异于点 与点
与点
 ,求
,求 的值;
的值; ,求
,求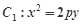 的焦点在抛物线
的焦点在抛物线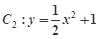 上.
上.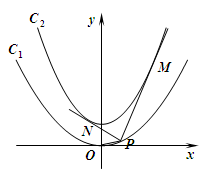
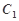 的方程及其准线方程;
的方程及其准线方程;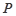 作抛物线
作抛物线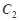 的两条切线
的两条切线 、
、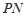 , 切点为
, 切点为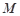 、
、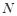 .若
.若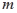 ,且
,且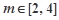 ,求
,求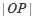 的取值范围.
的取值范围.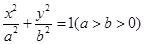 的离心率为
的离心率为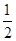 ,右焦点到直线
,右焦点到直线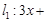
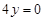 的距离为
的距离为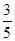 .
.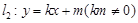 与椭圆C交于A、B两点,且线段AB中点恰好在直线
与椭圆C交于A、B两点,且线段AB中点恰好在直线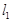 上,求△OAB的面积S的最大值.(其中O为坐标原点).
上,求△OAB的面积S的最大值.(其中O为坐标原点).