题目内容
过点C(0,1)的椭圆 的离心率为
的离心率为 ,椭圆与x轴交于两点
,椭圆与x轴交于两点 、
、 ,过点C的直线
,过点C的直线 与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(I)当直线 过椭圆右焦点时,求线段CD的长;
过椭圆右焦点时,求线段CD的长;
(II)当点P异于点B时,求证: 为定值.
为定值.
(I) (II)
(II) =4
=4
解析试题分析:(Ⅰ)由已知得 ,解得
,解得 ,所以椭圆方程为
,所以椭圆方程为 .
.
椭圆的右焦点为 ,此时直线
,此时直线 的方程为
的方程为  ,代入椭圆方程得
,代入椭圆方程得 ,解得
,解得 ,代入直线
,代入直线 的方程得
的方程得  ,所以
,所以  ,故
,故 .
.
(Ⅱ)当直线 与
与 轴垂直时与题意不符.
轴垂直时与题意不符.
设直线 的方程为
的方程为 .代入椭圆方程得
.代入椭圆方程得 .
.
解得 ,代入直线
,代入直线 的方程得
的方程得 ,
,
所以D点的坐标为 .
.
又直线AC的方程为 ,又直线BD的方程为
,又直线BD的方程为 ,联立得
,联立得 因此
因此 ,又
,又 .所以
.所以 .故
.故 为定值.
为定值.
考点:直线与圆锥曲线的综合问题 平面向量数量积的运算 椭圆的简单性质.
点评:本题主要考察了由椭圆的性质求解椭圆方程,直线与曲线相交的弦长公式的应用及向量的数量积的坐标表示的应用,属于圆锥曲线问题的综合应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 有相同的焦点,与双曲线
有相同的焦点,与双曲线 有相同渐近线,求双曲线方程.
有相同渐近线,求双曲线方程. 的顶点为原点,其焦点
的顶点为原点,其焦点 到直线
到直线 的距离为
的距离为 .设
.设 为直线
为直线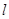 上的点,过点
上的点,过点 ,其中
,其中 为切点.
为切点. 为直线
为直线 的方程;
的方程; 的最小值.
的最小值. 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4, ),判断点
),判断点 是曲线
是曲线 ,短轴长为4
,短轴长为4 .
.
 ,直线PB的斜率为
,直线PB的斜率为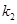 ,判断
,判断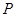 到两点
到两点 ,
, 的距离之和等于4,设点
的距离之和等于4,设点 ,直线
,直线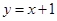 与轨迹
与轨迹 两点.
两点.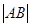 的值.
的值.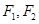 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆上,且满足
也在椭圆上,且满足 (
( 是坐标原点),
是坐标原点), ,若椭圆的离心率为
,若椭圆的离心率为 .
. 的面积等于
的面积等于 与(1)中的椭圆相交于不同的两点
与(1)中的椭圆相交于不同的两点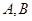 ,已知点
,已知点 ),点
),点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 ,求
,求 的值.
的值. 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为 ,点M是椭圆C上一点,
,点M是椭圆C上一点, 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为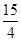 .
. 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线 与圆O的位置关系.
与圆O的位置关系. 的中心在原点,焦点在
的中心在原点,焦点在 轴上.若椭圆上的点
轴上.若椭圆上的点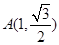 到焦点
到焦点 、
、 的距离之和等于4.
的距离之和等于4.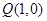 的直线与椭圆交于两点
的直线与椭圆交于两点 、
、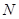 ,当
,当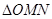 的面积取得最大值时,求直线
的面积取得最大值时,求直线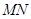 的方程.
的方程.