Question

（2013•枣庄二模）设f（x）=ax+cosx（x∈R）．
（1）若a=

1

2

，试求出函数f（x）的单调区间；
（2）若对任意x≥0，都有x+sin2x+cosx≤f（x）成立，求实数a的取值范围．

Answer 1

分析：（1）a=

1

2

时，f′（x）=

1

2

-sinx，解不等式f′（x）＞0，f′（x）＜0即可得到函数的单调区间；
（2）问题转化为?x≥0，（1-a）x+sin2x≤0，求实数a的取值范围．令g（x）=（1-a）x+sin2x，则g（x）≤0在[0，+∞）上恒成立，g（0）=0，当g（x）在[0，+∞）上单调递减满足题意，此时求出a≥3；当a＜3时，分下列两种情况讨论：①当a＜-1时，由导数可判断g（x）在[0，+∞）上递增，易知此时不合题意；②当-1≤a＜3时，令g′（x）＞0，借助三角函数图象可求g（x）的增区间，由此可判断此时不合题意；

解答：解：（1）f′（x）=a-sinx，a=

1

2

时，f′（x）=

1

2

-sinx，
f′（x）＞0?sinx＜

1

2

?2kπ-

7

6

π＜x＜2kπ+

7

6

π，k∈z，f′（x）＜0?sinx＞

1

2

?2kπ+

π

6

＜x＜2kπ+

5

6

π，k∈z，
所以，函数f（x）的增区间为（2kπ-

7

6

π，2kπ+

7

6

π），k∈z；减区间为（2kπ+

π

6

，2kπ+

5

6

π），k∈z．
（2）x+sin2x+cosx≤f（x）?x+sin2x≤ax?（1-a）x+sin2x≤0，
所以，问题转化为?x≥0，（1-a）x+sin2x≤0，求实数a的取值范围．
令g（x）=（1-a）x+sin2x，依题意，g（x）≤0在[0，+∞）上恒成立．
因为g（0）=0，要使g（x）≤0在[0，+∞）上恒成立，只要g（x）在[0，+∞）上单调递减即可，
这样，g′（x）=（1-a）+2cos2x≤0在[0，+∞）上恒成立即可，
于是，（1-a）≤-2cos2x在[0，+∞）上恒成立．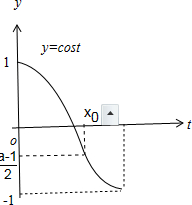
所以，1-a≤{-2cos2x}_min（x∈[0，+∞））=-2，即a≥3．
可见a≥3符合题意．
当a＜3时，分下列两种情况讨论：
①当a＜-1时，g′（x）=（1-a）+2cos2x＞1+1+2cos2x=2（1+cos2x）≥0，
因此，g（x）在[0，+∞）上为增函数，于是，当x＞0时，g（x）＞g（0）=0，
所以，a＜-1不符合题意；
②当-1≤a＜3时，令g′（x）=（1-a）+2cos2x＞0，则有cos2x＞

a-1

2

，
而-1≤

a-1

2

＜1，由函数y=cost在[0，π]上的图象知存在唯一的x₀∈（0，π]，使得cosx₀=

a-1

2

，
由右图，可知当2x∈（0，x₀），即x∈（0，

x0

2

）时，
有cos2x＞

a-1

2

，这时g′（x）＞0对区间（0，

x0

2

）内的任一x成立，
所以，函数g（x）在区间（0，

x0

2

）上单调递增，
又g（0）=0，所以，当x∈（0，

x0

2

）时，有g（x）＞0，
可见，-1≤a＜3不符合题意．
综上，满足题意的实数a的取值范围为a≥3．

点评：本题考查利用导数研究函数的单调性、在闭区间上的最值、三角函数等知识，考查分类讨论思想、数形结合思想，考查学生综合运用所学知识分析解决问题的能力，难度较大．