Question

光线从A(-3,4)点出发,到x轴上的点B后,被x轴反射到y轴上的C点,又被y轴反射,这时反射光线恰好过D(-1,6)点,求直线BC的方程.

Answer 1

思路分析：此题涉及物理学中光学的有关知识,解答本题可利用反射角等于入射角这一条件得出入射光线与反射光线所在直线的斜率之间的关系来解答.

解法一：如图,由题设知点B在原点O的左侧,设点B坐标为(a,0).

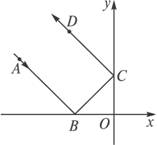
由反射角等于入射角这一物理知识可得k_AB=-k_BC且k_BC=-k_CD.

∵k_AB=-,

∴k_BC=,k_CD=-.

∴直线BC方程为y-0=(x-a),

即4x-(3+a)y-4a=0.

在方程4x-(3+a)y-4a=0中,令x=0,

可得C点坐标为(0,-),

则k_CD=-.

∴-=-,解得a=-.

因此直线BC的方程为5x-2y+7=0.

解法二：如图,作点A(-3,4)关于x轴的对称点A′(-3,-4),

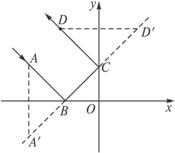
作点D(-1,6)关于y轴的对称点D′(1,6).

由物理及平面几何知识得A′、B、C、D′四点共线.

因为直线A′D′的方程为,

即5x-2y+7=0,

所以直线BC的方程为5x-2y+7=0.