题目内容
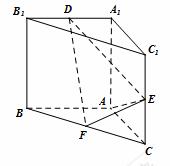
直三棱柱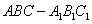 中,
中,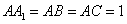 ,
,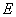 ,
,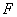
分别是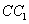 、
、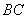 的中点,
的中点,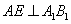 ,
, 为棱
为棱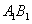 上的点.
上的点.
(1)证明: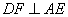 ;
;
(2)是否存在一点 ,使得平面
,使得平面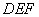 与平面
与平面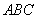 所成锐二面角的余弦值为
所成锐二面角的余弦值为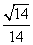 ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
(1)见解析;(2)当点 为
为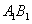 中点时,满足要求.
中点时,满足要求.
解析:(1)证明: ,
,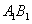 ∥
∥
 又
又

 面
面 又
又 面
面
 ………2分
………2分
以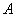 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系 
则 ,
, ,
, ,
, ,
,
设 ,
, 且
且 ,即:
,即:


 ………5分
………5分


 ………6分
………6分
(2)假设存在,设面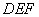 的法向量为
的法向量为  ,
,
则 


 即:
即:  令
令
 . ………8分
. ………8分
由题可知面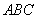 的法向量
的法向量 ………9分
………9分
 平面
平面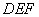 与平面
与平面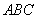 所成锐二面的余弦值为
所成锐二面的余弦值为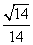
 即:
即:
 或
或 (舍) ………11分
(舍) ………11分
 当点
当点 为
为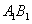 中点时,满足要求. ………12分
中点时,满足要求. ………12分

从某高中随机选取5名高二男生,其身高和体重的数据如下表所示:
| 身高 x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 63 | 66 | 70 | 72 | 74 |
由表可得回归直线方程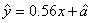 ,据此模型预报身高为
,据此模型预报身高为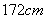 的男生的体重大约为( )
的男生的体重大约为( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg

 的值为
的值为 D.
D.

 ~
~ ,若
,若 ,则
,则 ____________.
____________.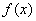 =
= .
.  的解集;
的解集; 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数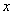 的取值范围.
的取值范围. 内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为
内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为 B、6
B、6 C、
C、 D、2
D、2
 。
。 时,解不等式
时,解不等式 ;
; ,求
,求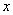 的取值范围。
的取值范围。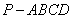 的底面为菱形,
的底面为菱形,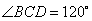 ,
,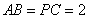 ,
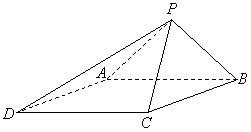
,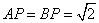 .
.

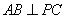 ;
;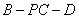 的余弦值.
的余弦值.