题目内容
若数列{an}满足：存在正整数T，对于任意正整数n都有an+T=an成立，则称数列{an}为周期数列，周期为T．已知数列{an}满足a1=m（m＞0），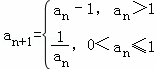
则下列结论中错误的是（ ）
|
| A． | 若a3=4，则m可以取3个不同的值 |
|
| B． | 若 |
|
| C． | ∀T∈N*且T≥2，存在m＞1，使得{an}是周期为T的数列 |
|
| D． | ∃m∈Q且m≥2，使得数列{an}是周期数列 |
，则数列{an}是周期为3的数列D解：对于选项A，因为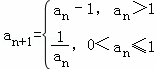，所以
，
因为a3=4，所以a2=5或
，又因为
，a1=m，所以m=6或m=
或m=
，所以选项A正确；
对于选项B，
＞1，所以
；所以
，所以
，
所以数列{an}是周期为3的数列，所以选项B正确；对于选项C，当B可知当＞1时，数列{an}是周期为3的周期数列，所以C正确．故错误的是D．故选D．
练习册系列答案
相关题目
，设P、Q为△ABC内的两点，且
，
，则△ABP的面积与△ABQ的
面积之比为 ．
把函数g(x)=f(x)-x的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为( )A.an=
B.an=n-1C.an=n(n-1) D.an=2n-2
，
，
，则数列
成 （ ） 
成等差数列，则下列不等式一定成立的是（ ）
B.
C.
D.
设函数y=f（x）的定义域为D，若对于任意x1，x2∈D且x1+x2=2a，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）图象的对称中心．研究并利用函数f（x）=x3﹣3x2﹣sin（πx）的对称中心，可得
=（ ）
|
| A． | 4023 | B． | ﹣4023 | C． | 8046 | D． | ﹣8046 |
的公差
且
，则数列
项和
取得最大值时的项数
的公差
，且
成等比数列，则
（ ）
B、
C、
D、
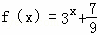，则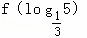
的值等于 ．