题目内容
2.已知函数$f(x)=\left\{{\begin{array}{l}{{{log}_2}x,x>0}\\{{3^x},x≤0}\end{array}}\right.$则$f(\frac{1}{4})$的值是-2.分析 将x=$\frac{1}{4}$代入函数的表达式,求出函数值即可.
解答 解:f($\frac{1}{4}$)=${log}_{2}^{{2}^{-2}}$=-2,
故答案为:-2.
点评 本题考查了求函数值问题,考查分段函数以及对数函数的性质,是一道基础题.

练习册系列答案
相关题目
14.在数列{an}中,a1=1,a2=5,an+2=an+1-an(n∈N),则a100等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | 0 |
17.从点P(-2,1)向圆x2+y2-2x-2my+m2=0作切线,当切线长最短时,m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x2的值及函数f(x)的解析式;
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
| x | x1 | $\frac{π}{12}$ | x2 | $\frac{7π}{12}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 1 | 4 | 1 | -2 | 1 |
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
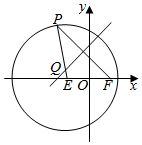 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.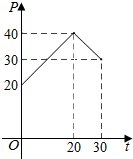 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.