题目内容
设函数f(x)=
,其中[x]表示不超过x的最大整数,如[-1.2]=-2,[1.2]=1,[1]=1,若直线ky=x+1(k>0)与函数y=f(x)的图象恰有两个不同的交点,则k的取值范围是( )
|
| A、[2,3) |
| B、[3,∞) |
| C、[2,3] |
| D、(2,3] |
考点:函数的零点与方程根的关系,分段函数的应用
专题:综合题,函数的性质及应用
分析:画出函数f(x)=
,g(x)=
(x+1)(k>0)的图象,利用斜率和题意可得:kPA≤
<kPC,解出k的取值范围即可.
|
| 1 |
| k |
| 1 |
| k |
解答:
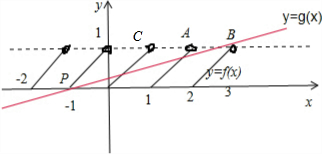 解:画出函数f(x)=
解:画出函数f(x)=
,g(x)=
(x+1)(k>0)的图象,若直线ky=x+1(k>0)与函数y=f(x)的图象恰有两个不同的交点,
结合图象可得:kPA≤
<kPC,
∵kPA=
=
,kPC=
=
.
∴2<k≤3.
故选D.
 解:画出函数f(x)=
解:画出函数f(x)=
|
| 1 |
| k |
结合图象可得:kPA≤
| 1 |
| k |
∵kPA=
| 1 |
| 2-(-1) |
| 1 |
| 3 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
∴2<k≤3.
故选D.
点评:正确画出函数图象、得出斜率k满足的条件是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
函数f(x)=sinxsin(
+x)-x的零点的个数为( )
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
在△ABC中,角A,B,C的对边分别为a,b,c,且b2=a2+bc,A=
,则内角C=( )
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
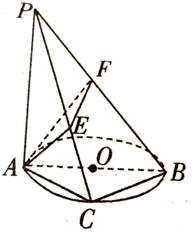 如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.
如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.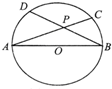 如图,AB是圆O的直径,过A、B的两条弦AC和BD相交于点P,若圆O的半径是3,则AC•AP+BD•BP的值
如图,AB是圆O的直径,过A、B的两条弦AC和BD相交于点P,若圆O的半径是3,则AC•AP+BD•BP的值