题目内容
设数列{an}满足an+1=2an+n2-4n+1.
(1)若a1=3,求证:存在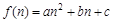 (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
(1)若a1=3,求证:存在
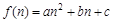 (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
(1) ,(2)
,(2)
 ,(2)
,(2)
试题分析:(1)解一般数列问题,主要从项的关系进行分析.本题项的关系是:
 型,解决方法为:构造等比数列
型,解决方法为:构造等比数列 ,再利用
,再利用 等式对应关系得出
等式对应关系得出 的解析式,(2)解等差数列问题,主要从待定系数对应关系出发.令
的解析式,(2)解等差数列问题,主要从待定系数对应关系出发.令 ,则利用
,则利用 等式对应关系得出
等式对应关系得出 ,再利用等差数列前n项和公式
,再利用等差数列前n项和公式 得
得
试题解析:解(1)

设
 2分
2分也即
 4分
4分
 6分
6分
所以存在
 使数列
使数列 是公比为2的等比数列 8分
是公比为2的等比数列 8分
则
 10分
10分(2)
 即
即
 即
即 12分
12分 14分
14分 是等差数列,
是等差数列,  16分
16分
练习册系列答案
相关题目
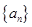 的前
的前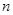 项和为
项和为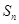 ,满足
,满足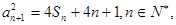 且
且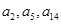 恰好是等比数列
恰好是等比数列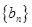 的前三项.
的前三项.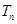 ,若对任意的
,若对任意的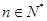 ,
,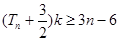 恒成立,求实数
恒成立,求实数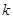 的取值范围.
的取值范围.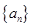 ,
,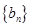 满足
满足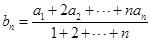
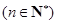 .
.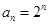 ,求数列
,求数列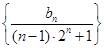 的前
的前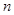 项和
项和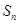 .
. 的前n项和为
的前n项和为 ,且
,且 ,则
,则 ( )
( ) 中,若
中,若 ,则该数列的前15项的和为____________.
,则该数列的前15项的和为____________. ,Sn为数列{an}的前n项和,则S8= ;S4n= 。
,Sn为数列{an}的前n项和,则S8= ;S4n= 。 中,
中, ,
, ,则
,则 =___________.
=___________. 中,
中, ,则数列
,则数列 ( )
( )