题目内容
已知函数 ,
, .若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是 .
.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是 .
【答案】分析:对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),等价于f(x)min≥g(x)min,于是问题转化为求函数f(x),g(x)的最小值问题.
解答:解:当x∈[1,2]时,
f(x)= =
= ≥3
≥3 =3,
=3,
当且仅当 即x=1时取等号,所以f(x)min=3.
即x=1时取等号,所以f(x)min=3.
g(x)= -m在[-1,1]上单调递减,所以
-m在[-1,1]上单调递减,所以 ,
,
对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),等价于f(x)min≥g(x)min,
即3≥ -m,解得m≥-
-m,解得m≥- .
.
故答案为:[- ,+∞).
,+∞).
点评:本题考查函数恒成立问题,解决的常用方法是转化为函数的最值问题进行处理.
解答:解:当x∈[1,2]时,
f(x)=
 =
= ≥3
≥3 =3,
=3,当且仅当
 即x=1时取等号,所以f(x)min=3.
即x=1时取等号,所以f(x)min=3.g(x)=
 -m在[-1,1]上单调递减,所以
-m在[-1,1]上单调递减,所以 ,
,对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),等价于f(x)min≥g(x)min,
即3≥
 -m,解得m≥-
-m,解得m≥- .
.故答案为:[-
 ,+∞).
,+∞).点评:本题考查函数恒成立问题,解决的常用方法是转化为函数的最值问题进行处理.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
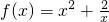 ,
, .若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是________.
.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是________.