题目内容
已知数列{an}的前n项和Sn与通项an满足Sn=
-an.
(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=
+
+…+
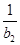,求T2012;
(3)若cn=an·f(an),求{cn}的前n项和Un.
-an.(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=
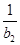++…+,求T2012;(3)若cn=an·f(an),求{cn}的前n项和Un.
(1) an=
n (2) 
(3) Un=-
+·
n+
n·n+1
n (2) (3) Un=-+·n+n·n+1解:(1)当n=1时,a1=
,当n≥2时,an=Sn-Sn-1=
-an-+an-1,所以an=
an-1,即数列{an}是首项为
,公比为的等比数列,故an=
n.(2)由已知可得f(an)=log3
n=-n.则bn=-1-2-3-…-n=-
,故
=-2(
-
),又Tn=-2[(1-
)+(-)+…+(-)]=-2(1-
),所以T2012=-
.(3)由题意得cn=-n·
n,故Un=c1+c2+…+cn
=-[1×
1+2×2+…+n×n],则
Un=-[1×2+2×3+…+n×n+1],两式相减可得
Un=-[1+2+…+n-n·n+1]=-
[1-n]+n·n+1=-
+·n+n·n+1,则Un=-
+·n+n·n+1.
练习册系列答案
开心蛙口算题卡系列答案
相关题目
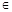N*，都有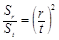
．
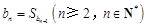，求证：数列
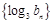为等比数列；
．
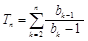和
中，已知
.
，求数列
的前n项和
.
=an,则a3= ;{an}的前n项和Sn= . 
的等比数列{an}的前n项和为Sn,则( )
；④f(x)＝ln(x)．