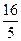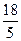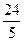题目内容
(本小题满分12分)已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证:函数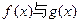 图象交于不同的两点;
图象交于不同的两点;
(2)设(1)问中交点为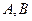 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。
(1)求证:函数
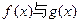 图象交于不同的两点;
图象交于不同的两点;(2)设(1)问中交点为
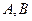 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。(1)证明略
(2)(
 )
)(1)由
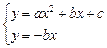 消去y得ax2+2bx+c=0
消去y得ax2+2bx+c=0Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)=4[(a+
 c2]
c2]∵a+b+c=0,a>b>c,∴a>0,c<0
∴
 c2>0,∴Δ>0,即两函数的图象交于不同的两点(6分)
c2>0,∴Δ>0,即两函数的图象交于不同的两点(6分)(2)解设方程ax2+2bx+c=0的两根为x1和x2,则x1+x2=-
 ,x1x2=
,x1x2=
|A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2
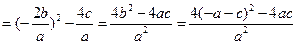
 (8分)
(8分)∵a>b>c,a+b+c=0,a>0,c<0
∴a>-a-c>c,解得
 ∈(-2,-
∈(-2,- )(10分)
)(10分)∵
 的对称轴方程是
的对称轴方程是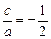
 ∈(-2,-
∈(-2,- )时,为减函数
)时,为减函数∴|A1B1|2∈(3,12),故|A1B1|∈(
 )(12分)
)(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有两个相等的实根。(1)求函数
有两个相等的实根。(1)求函数 的解析式;
的解析式; 的奇偶性,并证明。
的奇偶性,并证明。 ,
,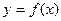 与
与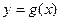 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若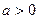 ,试建立
,试建立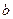 关于
关于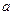 的函数关系式;
的函数关系式;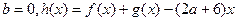 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求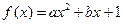
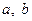 为实数,
为实数,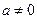 ,
,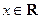 ),
),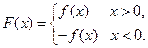
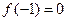 ,且函数
,且函数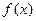 的值域为
的值域为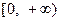 ,求
,求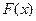 的表达式;
的表达式;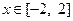 时,
时,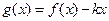 是单调函数,求实数
是单调函数,求实数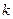
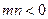 ,
,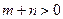 ,
,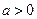 ,且函数
,且函数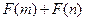 是
是 ?
?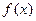 满足:
满足: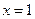 时有极值;
时有极值;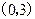 ,且在该点处的切线与直线
,且在该点处的切线与直线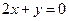 平行.求
平行.求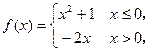 若
若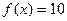 ,则
,则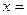
 为开口向下的抛物线,且对任意x∈R都有f(1+x)=f(1-x).若向量
为开口向下的抛物线,且对任意x∈R都有f(1+x)=f(1-x).若向量 ,
,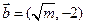 ,则满足不等式
,则满足不等式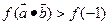 m取值范围 。
m取值范围 。 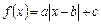 满足①函数
满足①函数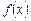 的图象关于
的图象关于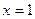 对称;②在
对称;②在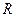 上有大于零的最大值;③函数
上有大于零的最大值;③函数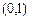 ;④
;④ ,试写出一组符合要
,试写出一组符合要 求的
求的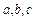 的值
的值 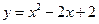 与
与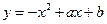
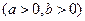 在它们的一个交点处切线互相垂直,则
在它们的一个交点处切线互相垂直,则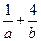 的最小值为( )
的最小值为( )