题目内容

13．已知函数f（x）的定义域为[a，b]，在同一坐标系下，函数y=f（x）的图象与直线x=1的交点个数为0或1．

分析 根据函数的定义，可得本题结论

解答 解：根据函数的定义，对于定义域内的任一自变量x，存在唯一的函数值y与之对应．
（1）当1∈[a，b]时，f（1）的值唯一，
故函数y=f（x），x∈[a，b]的图象与直线x=1的交点为（1，f（1）），唯一的；
（2）当1∉[a，b]时，f（1）的值无意义，
故函数y=f（x），x∈[a，b]的图象与直线x=1的交点不存在；
故答案为：0或1

点评 本题考查的是函数的定义，要求准确理解函数定义，本题属于基础题．

练习册系列答案
相关题目
3．已知椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左、右焦点分别为F1，F2，过F1且倾斜角为45°的直线l与椭圆相交于A，B两点．则AB的中点坐标（　　）
A．（-$\frac{3}{5}$，$\frac{2}{5}$）B．（1，-1）C．（-1，$\frac{2}{5}$）D．（-1，1）
4．定义在R上的偶函数f（x），满足f（x+1）=-f（x），且f（x）在[-1，0]上是增函数，
①f（x）为周期函数；      
②f（x）的图象关于x=1对称；      
③f（x）在[0，1]上为增函数；
④f（x）在[1，2]上为减函数；   
⑤f（2）=f（0）．
则上述说法正确的有①②⑤．
1．设集合A={0，2，3}，B={x+1，x}，A∩B={3}，则实数x的值为3．
8．已知函数f（x）=$\left\{\begin{array}{l}{2^x}，x≤1\\ ln（{x-1}），1＜x＜2\end{array}$，若存在实数a，当x＜2时，f（x）≤ax+b恒成立，则实数b的取值范围是（　　）
A．[1，+∞）B．[2，+∞）C．[3，+∞）D．[4，+∞）
18．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）（ω＞0，-$\frac{π}{2}$≤φ＜$\frac{π}{2}$）图象的一个对称中心为（$\frac{π}{12}$，0），且图象上相邻两条对称轴间的距离为$\frac{π}{2}$．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调减区间；
（3）若f（$\frac{α}{2}$）=$\frac{\sqrt{3}}{4}$（$\frac{π}{6}$＜α＜$\frac{2π}{3}$），求cos（α+$\frac{3π}{2}$）的值．
5．（理科）如图，已知四棱锥P-ABCD的底面ABCD为菱形，且∠ABC=60°，AB=PC=2，PA=PB=$\sqrt{2}$，
（1）求证：平面PAB⊥平面ABCD；
（2）求二面角P-AC-B的余弦值．
2．已知数列{an}是首项为1，公比为$\frac{1}{2}$的等比数列，令Sn=a1+a2+…+an，Tn=a1（a1+a2+…+an）+a2（a2+a3+…+an）+…+an-1（an-1+an）+an2．若对一切正整数n，都有Tn＞c•Sn2，则c的取值范围是（-∞，$\frac{4}{3}$]．
3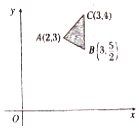．如图，已知点（x，y）在△ABC所包围的阴影部分区域内（包含边界），若B（3，$\frac{5}{2}$）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（　　）
A．[-$\frac{1}{2}$，+∞）B．[0，+∞）C．（-∞，-$\frac{1}{2}$]D．[-$\frac{1}{2}$，0]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网