题目内容
设函数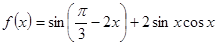
（1）求函数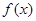
的周期和单调递增区间；
（2）设A,B,C为
ABC的三个内角，若AB=1， 
，
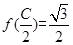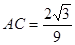，求s1nB的值.
（1）周期为
,单调递增区间为
（2）
解析试题分析：（1）用两角和差公式、二倍角公式和化一公式将函数
化简为
的形式，根据周期公式
求其周期；将整体角
代入正弦的单调增区间内，即可解得函数的增区间。（2）根据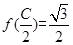可得角
，根据正弦定理可得
。
试题解析：=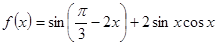
（1）函数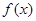的周期为.
令
，则
∴函数f(x)的单调递增区间为
（2）由已知
， 因为
所以
，
，∴s1nC =
.
在
中，由正弦定理，
，得.
考点：1三角函数的化简；2正弦定理。
练习册系列答案
相关题目
＋
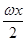sin ωx－3(ω＞0)在一个周期内的图象如图所示，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为正三角形．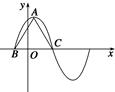
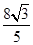，且x0∈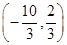
，求f(x0＋1)的值．
．
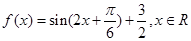的最小正周期和单调增区间．
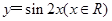的图象经过怎样的变换得到？
．
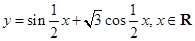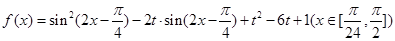其最小值为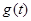
.
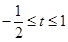时，要使关于
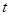的方程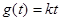
有一个实根，求实数
的取值范围．
.
的最大值，并写出
的取值集合；
中，角
的对边分别为
若
求实数
的最小值.
．
的最小正周期和值域；
中，角
的对边分别为
，若
且
，
，求
和
．
.
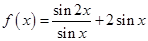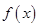的定义域和最小正周期；
，
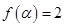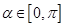，求
的值.
，
，设函数
．
的最小正周期；
上的最小值和最大值．