题目内容
已知函数
.
(1)求函数
的最大值，并写出取最大值时
的取值集合；
（2）已知
中，角
的对边分别为
若
求实数
的最小值.
（1）
；（2）实数取最小值1
解析试题分析：（1）先用诱导公式化为二倍角，再用两角和的正弦化为一个三角函数，然后求使得
成立时x的集合即可；
(2)利用已知中求出A角的值，在△ABC中根据余弦定理用含b，c的代数式表示a的平方，再由
b与c的和为定值利用均值不等式从而求出a的最小值.
试题解析：(1)
.
∴函数的最大值为
.要使取最大值，则
，解得
.
故的取值集合为. 6分
（2）由题意，
，化简得
，
，∴
，∴
在中，根据余弦定理，得
.
由
，知
，即
.
∴当
时，实数取最小值
12分
考点：(1)三角函数的最值(2)余弦定理和基本不等式.
练习册系列答案
浙江名校名师金卷系列答案
相关题目
．
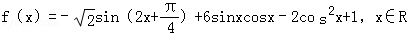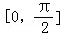上的最大值和最小值．
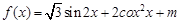，其定义域为
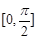，最大值为6.
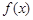的单调递增区间.
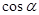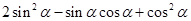的值；
的值.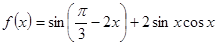
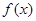的周期和单调递增区间；
ABC的三个内角，若AB=1， 
，
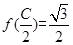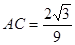，求s1nB的值.
.
的定义域及最小正周期；
的最大值为3，最小值为
.
的值；
时，函数
的值域.
)的图象与x轴的交点中，相邻两个交点之间的距离为
，－2)．
，
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,
),求f(θ)的值;
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.