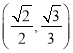题目内容
【题目】椭圆中心为坐标原点O,对称轴为坐标轴,且过M(2, ![]() ) ,N(
) ,N(![]() ,1)两点,
,1)两点,
(I)求椭圆的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
【答案】(1)![]() (2)
(2)![]() ,
, ![]()
【解析】试题分析:(Ⅰ)由椭圆的离心率及过点过M(2, ![]() ) ,N(
) ,N(![]() ,1)列出方程组求出
,1)列出方程组求出![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程.
的方程.
(2)假设存在这样的圆,设该圆的切线为![]() 与椭圆联立,得
与椭圆联立,得![]() 由此利用根的判别式、韦达定理、圆的性质,结合已知条件能求出
由此利用根的判别式、韦达定理、圆的性质,结合已知条件能求出![]() 的取值范围.
的取值范围.
试题解析:(1)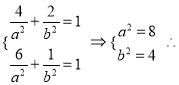
![]()
(2)假设存在这样的圆,设该圆的切线为y=kx+m,与![]() 联立消y得(1+2k2)x2+4kmx+2m2﹣8=0
联立消y得(1+2k2)x2+4kmx+2m2﹣8=0
当△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0
![]()
因为![]() ,所以
,所以![]()
所以3m2﹣8k2﹣8=0,由△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0 得
△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0
代入化简得![]()
又y=kx+m与圆心在原点的圆相切,所以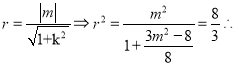 所求圆
所求圆 ![]() ,直线AB斜率不存在时也满足.
,直线AB斜率不存在时也满足.
当![]() 时,
时, 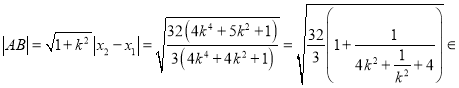
![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]()

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目