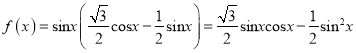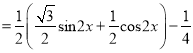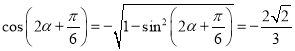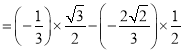Question

【题目】函数是定义在上的奇函数，且.

（1）确定的解析式；

（2）判断并证明在上的单调性；

（3）解不等式.

Answer 1

【答案】(1) ， ；(2) 是上增函数，证明见解析；(3) .

【解析】试题分析：（1）若奇函数在x=0处有定义，则f（0）=0，代入即可得b，再由

代入即可得a值；（2）因为函数为奇函数，故只需判断x＞0时函数的单调性即可，利用单调性定义即可证明；（3）利用函数的单调性和奇偶性将不等式中的f脱去，等价转化为关于t的不等式组，解之即可.

试题解析：(1)由函数是定义在上的奇函数知，所以，

经检验， 时是上的奇函数，满足题意.

又，解得，故， .

(2) 是上增函数.证明如下：

在任取且，则， ， ， ，

所以 ，即，

所以是上增函数.

(3) 因为是上的奇函数，所以由得， ，

又是上增函数，

所以 解得，从而原不等式的解集为.