题目内容
【题目】若关于x的不等式a﹣ax>ex(2x﹣1)(a>﹣1)有且仅有两个整数解,则实数a的取值范围为( )
A.(﹣ ![]() ,
, ![]() ]
]
B.(﹣1, ![]() ]
]
C.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
D.(﹣ ![]() ,﹣
,﹣ ![]() )
)
【答案】C
【解析】解:由a﹣ax>ex(2x﹣1)(a>﹣1),
设g(x)=a﹣ax,h(x)=ex(2x﹣1),
h′(x)=ex(2x﹣1)+2ex=ex(2x+1),
由h′(x)>0得x>﹣ ![]() ,
,
由h′(x)<0得x<﹣ ![]() ,
,
即当x=﹣ ![]() 时,函数h(x)取得极小值h(﹣
时,函数h(x)取得极小值h(﹣ ![]() ),
),
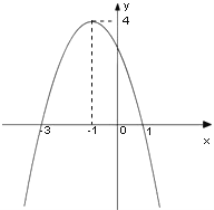
作出g(x)的图象如图:
若g(x)>h(x)解集中的整数恰为2个,
则x=0,﹣1是解集中的三个整数,
则满足 ![]() ,即
,即  ,
,
则 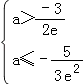 ,即﹣
,即﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,
,
即实数a的取值范围是(﹣ ![]() ,﹣
,﹣ ![]() ],
],
故选:C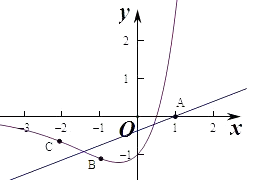

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目