题目内容

设（
2
+x）10=a0+a1x+a2x2+…+a10x10，则 （a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2的值为
1
1
．
分析：利用赋值法分别令x=1和x=-1，即可求出（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2的值．
解答：解：∵（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2=（a0+a2+a4+…+a10+a1+a3+a5+…+a9）[（a0+a2+a4+…+a10）-（a1+a3+a5+…+a9）]，
∴令x=1，则a0+a1+a2+…+a10=[（a0+a2+a4+…+a10）+（a1+a3+a5+…+a9）]=（
2
+1）10，
令x=-1，则a0-a1+a2-…+a10=[（a0+a2+a4+…+a10）-（a1+a3+a5+…+a9）]=（
2
-1）10，
∴两式相乘得：（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2=）]=（
2
+1）10•（
2
-1）10=[（
2
）2-1]10=110=1．
故答案为：1．
点评：本题主要考查二项式定理的应用，利用赋值法是解决本题的关键，比较基础．
练习册系列答案
相关题目
设函数f(x)=(
1
2
)10-ax，a为常数，且f（3）=
1
2

（1）求a值；
（2）求使f（x）≥4的x值的取值范围；
（3）设g（x）=-
1
2
x+m，对于区间[3，4]上每一个x值，不等式f（x）＞g（x）恒成立，求实数m的取值范围．
仔细阅读下面问题的解法：
设A=[0，1]，若不等式21-x-a＞0在A上有解，求实数a的取值范围．
解：由已知可得  a＜21-x
令f（x）=21-x，不等式a＜21-x在A上有解，
∴a＜f（x）在A上的最大值
又f（x）在[0，1]上单调递减，f（x）max=f（0）=2
∴a＜2即为所求．
学习以上问题的解法，解决下面的问题：
（1）已知函数f（x）=x2+2x+3 （-2≤x≤-1）求f（x）的反函数及反函数的定义域A；
（2）对于（1）中的A，设g（x）=
10-x
10+x
x∈A，试判断g（x）的单调性；（不证）
（3）又若B={x|
10-x
10+x
＞2x+a-5}，若A∩B≠Φ，求实数a的取值范围．
设f（x）=
∫
1
0
 |x2-a2|dx．
（1）当0≤a≤1与a＞1时，分别求f（a）；
（2）当a≥0时，求f（a）的最小值．
设（-x）10=a+a1x+a2x2+…+a10x10，求（a+a2+…+a10）2（a1+a3+…+a9）2的值．
给出以下结论：（1）x，y∈R，若x2+y2=0，则x=0或y=0的否命题是假命题；
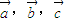（2）若非零向量两两成的夹角均相等，则夹角为0°或120°
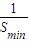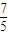
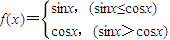（3）若（1+x）10=a+a1x+a2x2+…+a10x10，则a+a1+2a2+3a3+…10a10=10×29
（4）实数x，y满足4x2-5xy+4y2=5，设S=x2+y2，则+=
（5）函数为周期函数，且最小正周期T=2π
其中正确的结论的序号是：    （写出所有正确的结论的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网