题目内容
设（
-x）10=a+a1x+a2x2+…+a10x10，求（a+a2+…+a10）2（a1+a3+…+a9）2的值．
【答案】分析：令x=1可得：a+a1+a2+…+a10=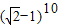
，再令x=-1可得 a-a1+a2-a3+…+a8-a9+a10=
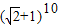．求得 a+a2+…+a10 和a1+a3+…+a9 的值，
可得 （a+a2+…+a10）2和（a1+a3+…+a9）2 的值，从而求得（a+a2+…+a10）2（a1+a2+…+a9）2的值．
解答：解：令x=1可得：a+a1+a2+…+a10=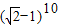
，再令x=-1可得 a-a1+a2-a3+…+a8-a9+a10=
．
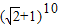由以上两式可得 a+a2+…+a10 =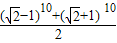
，a1+a3+…+a9=
，
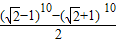∴（a+a2+…+a10）2 =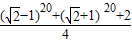
，（a1+a3…+a9）2=
，
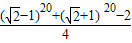∴（a+a2+…+a10）2（a1+a3+…+a9）2 =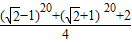
-
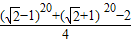=1．
点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于中档题．
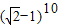，再令x=-1可得 a-a1+a2-a3+…+a8-a9+a10=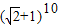．求得 a+a2+…+a10 和a1+a3+…+a9 的值，可得 （a+a2+…+a10）2和（a1+a3+…+a9）2 的值，从而求得（a+a2+…+a10）2（a1+a2+…+a9）2的值．
解答：解：令x=1可得：a+a1+a2+…+a10=
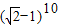，再令x=-1可得 a-a1+a2-a3+…+a8-a9+a10=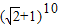．由以上两式可得 a+a2+…+a10 =
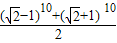，a1+a3+…+a9=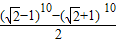，∴（a+a2+…+a10）2 =
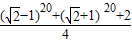，（a1+a3…+a9）2=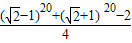，∴（a+a2+…+a10）2（a1+a3+…+a9）2 =
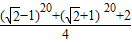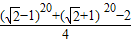-=1．点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于中档题．
练习册系列答案
相关题目
设e＜x＜10，记a=ln（lnx），b=lg（lgx），c=ln（lgx），d=lg（lnx），则a，b，c，d的大小关系（ ）
| A、a＜b＜c＜d | B、c＜d＜a＜b | C、c＜b＜d＜a | D、b＜d＜c＜a |
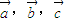两两成的夹角均相等，则夹角为0°或120°
+
=
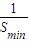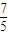
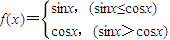为周期函数，且最小正周期T=2π