题目内容
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若过其右焦点F作倾斜角为45°的直线l与双曲线右支有两个不同的交点,则双曲线的离心率的范围是(1,$\sqrt{2}$).分析 要使直线与双曲线有两个交点,需使双曲线的其中一渐近线方程的斜率小于直线的斜率,即$\frac{b}{a}$<tan45°=1,求得a和b的不等式关系,进而转化成a和c的不等式关系,求得离心率的一个范围,最后根据双曲线的离心率大于1,综合可得求得e的范围.
解答 解:要使直线与双曲线有两个交点,需使双曲线的其中一渐近线方程的斜率小于直线的斜率,
即$\frac{b}{a}$<tan45°=1,即b<a
∴$\sqrt{{c}^{2}-{a}^{2}}$<a,
整理得c<$\sqrt{2}$a,
∴e=$\frac{c}{a}$<$\sqrt{2}$,
∵双曲线中e>1,
∴e的范围是(1,$\sqrt{2}$)
故答案为(1,$\sqrt{2}$).
点评 本题以双曲线为载体,考查了双曲线的简单性质.在求离心率的范围时,注意双曲线的离心率大于1.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
10.若二次函数y=-x2+bx+c的图象的对称轴是x=2,则有( )
| A. | f(1)≤f(2)≤f(4) | B. | f(2)>f(1)>f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)>f(2)>f(1) |
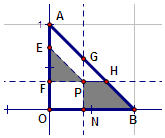 △AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.
△AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标. 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.