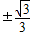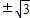Question

设直线l过点（-2，0），且与圆x²+y²=1相切，则l的斜率是（　　）

• A、±1
• B、±

  1

  2

• C、±

  3

  3

• D、±

  3

Answer 1

分析：首先根据已知圆判断其圆心与半径，然后解构成的直角三角形，求出夹角，继而求出倾斜角，解出斜率即可．

解答：解：∵直线l过点（-2，0），且与圆x²+y²=1相切
由圆得：圆心为（0，0），半径为1
∴构成的三角形的三边为：2，1，

3

，
解得直线与x轴夹角为30°的角
∴x的倾斜角为30°或150°
∴k=±

3

3

故选C．

点评：本题考查直线的斜率，直线与圆的位置关系，通过解直角三角形完成求直线l的斜率，属于基础题．