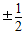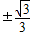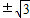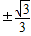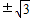Question

设直线l过点（2，0）且与曲线C：y=

1

x

相切，则l与C及直线x=2围成的封闭图形的面积为（　　）

• A、1n2-

  1

  2

• B、1-1n2
• C、2-1n2
• D、2-21n2

Answer 1

分析：利用导数的几何意义和斜率的计算公式得出切线的斜率，可得切线的方程，利用微积分基本定理即可得出．

解答：解：由曲线C：y=

1

x

，∴y′=-

1

x2

，设切点为P（x₀，y₀），则切线的斜率为-

1

x 2 0

=

1 x0

x0-2

解得x₀=1，
即切线的斜率k=-1．
∴切点为（1，1），因此切线方程为y=-（x-2）．
∴直线l与C及直线x=2围成的封闭图形的面积S=

∫

2 1

(

1

x

-2+x)dx=(lnx-2x+

1

2

x2)

|

2 1

=ln2-

1

2

．
故选A．

点评：熟练掌握导数的几何意义、切线的方程、斜率的计算公式、微积分基本定理是解题的关键．