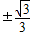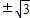题目内容
设直线l过点(-2,0)且与圆x2+y2=1相切,则l的斜率为______.
由圆x2+y2=1,得到圆心坐标为(0,0),半径r=1,
显然直线l的斜率存在,设直线l的斜率为k,
由直线l过点(-2,0),得到直线l的方程为:y=k(x+2),即kx-y+2k=0,
∵直线l与圆相切,∴圆心(0,0)到直线l的距离d=
=r=1,
两边平方整理得:4k2=k2+1,即k2=
,
则k=±
.
故答案为:±
显然直线l的斜率存在,设直线l的斜率为k,
由直线l过点(-2,0),得到直线l的方程为:y=k(x+2),即kx-y+2k=0,
∵直线l与圆相切,∴圆心(0,0)到直线l的距离d=
| |2k| | ||
|
两边平方整理得:4k2=k2+1,即k2=
| 1 |
| 3 |
则k=±
| ||
| 3 |
故答案为:±
| ||
| 3 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
设直线l过点(-2,0),且与圆x2+y2=1相切,则l的斜率是( )
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|