题目内容
5.求与椭圆4x2+9y2=36有相同的焦距,且离心率为$\frac{\sqrt{5}}{5}$的椭圆的标准方程.分析 设要求的椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$.由椭圆4x2+9y2=36化为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1,可得c.可得a,b2=a2-c2.即可得出.
解答 解:设要求的椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$.
由椭圆4x2+9y2=36化为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1,可得c=$\sqrt{9-4}$=$\sqrt{5}$.
∴a=5,b2=a2-c2=20.
∴要求的椭圆标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{20}=1$.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.x,y∈R,A={(x,y)|x2+y2=1},B={(x,y)|$\frac{x}{a}$-$\frac{y}{b}$=1,a>0,b>0},当A∩B只有1个元素时,a,b满足的关系式为( )
| A. | $\frac{1}{a}$+$\frac{1}{b}$=1 | B. | a2+b2=1 | C. | $\frac{1}{a^2}$+$\frac{1}{b^2}$=1 | D. | a+b=ab |
10.若函数f(x)=(2m-1)x${\;}^{{m}^{2}-2}$是幂函数,则 f(-2)=( )
| A. | -1 | B. | -2 | C. | 1 | D. | -$\frac{1}{2}$ |
15.函数f(x)=x2-2mx+5在区间[-2,+∞)上是增函数,则m的取值范围是( )
| A. | (-∞,-2] | B. | [-2,+∞) | C. | (-∞,-1] | D. | [-1,+∞) |
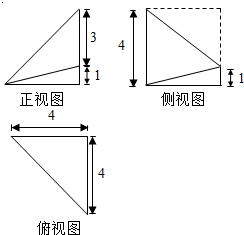 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.