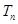题目内容
已知数列 中,
中, ,前
,前 项的和为
项的和为 ,对任意的
,对任意的 ,
, ,
, ,
, 总成等差数列.
总成等差数列.
(1)求 的值;
的值;
(2)求通项 ;
;
(3)证明: .
.
(1)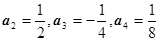 (2)
(2)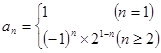
(3)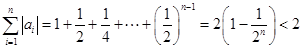
解析试题分析:(1) ,
, ,
, 总成等差数列,所以有
总成等差数列,所以有 ,令
,令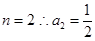 ,令
,令 ,令
,令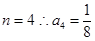 4分
4分
(2) 由已知可得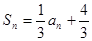 (
(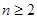 )
)
所以 (
(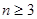 ) ,从第二项开始构成等比数列,公比为
) ,从第二项开始构成等比数列,公比为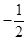 ,
,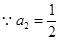

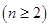

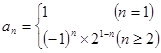 8分
8分
(3) 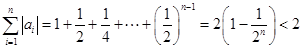 12分
12分
考点:数列求通项求和
点评:本题已知条件主要是关于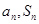 的关系式,由此求通项时借助于
的关系式,由此求通项时借助于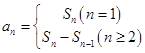
此外第二小题还可借助于第一问的结论,结合数学归纳法猜想并证明

练习册系列答案
相关题目
 .
.
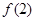 ,
,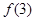 ,
,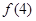 ,
,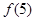 ;
;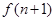 的关系,并求出
的关系,并求出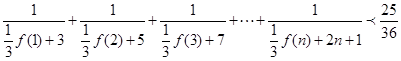 (
( ).
).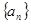 中,已知
中,已知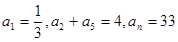 ,试求n的值
,试求n的值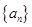 中,
中,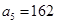 ,公比
,公比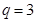 ,前
,前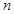 项和
项和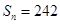 ,求首项
,求首项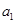 和项数
和项数 的前
的前 项和为
项和为 ,且满足
,且满足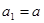 (
(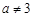 ),
),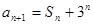 ,设
,设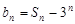 ,
,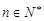 .
.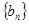 是等比数列;
是等比数列;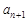 ≥
≥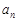 ,
,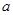 的最小值;
的最小值;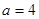 时,给出一个新数列
时,给出一个新数列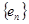 ,其中
,其中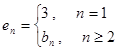 ,设这个新数列的前
,设这个新数列的前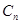 ,若
,若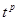 (
(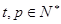 且
且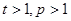 )的形式,则称
)的形式,则称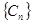 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由. 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
, ,
, .
.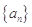 中,
中,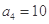 且
且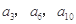 成等比数列,
成等比数列,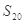 。
。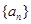 的前三项和为18,
的前三项和为18,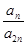 是一个与
是一个与 无关的常数,若
无关的常数,若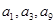 恰为等比数列
恰为等比数列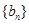 的前三项,(1)求
的前三项,(1)求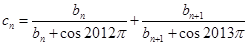 ,
,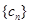 的前三
的前三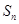 ,求证:
,求证: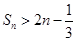
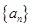 中,前
中,前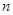 项和为
项和为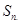 ,且
,且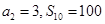 .
.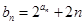 ,求数列
,求数列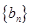 前
前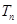 .
. 为递减的等差数列,
为递减的等差数列,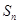 是数列
是数列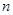 项和,且
项和,且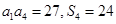 .
.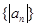 的前
的前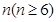 项和
项和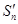
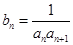 ,求数列
,求数列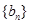 的前
的前