题目内容
观察以下三个等式:
sin215°-sin245°+sin15°cos45°=-
,
sin220°-sin250°+sin20°cos50°=-
,
sin230°-sin260°+sin30°cos60°=-
;
猜想出一个反映一般规律的等式: .
sin215°-sin245°+sin15°cos45°=-
| 1 |
| 4 |
sin220°-sin250°+sin20°cos50°=-
| 1 |
| 4 |
sin230°-sin260°+sin30°cos60°=-
| 1 |
| 4 |
猜想出一个反映一般规律的等式:
考点:归纳推理
专题:推理和证明
分析:对题设中给出的三个式子进行变形,总结规律,由此能求出反映一般规律的等式.
解答:
解:由已知得:
sin215°-sin2(15°+30°)+sin15°cos(15°+30°)=-
,
sin220°-sin2(20°+30°)+sin20°cos(20°+30°)=-
,
sin230°-sin2(30°+30°)+sin30°cos(30°+30°)=-
,
∴猜想出一个反映一般规律的等式:sin2θ-sin2(θ+30°)+sinθcos(θ+30°)=-
.
故答案为:sin2θ-sin2(θ+30°)+sinθcos(θ+30°)=-
.
sin215°-sin2(15°+30°)+sin15°cos(15°+30°)=-
| 1 |
| 4 |
sin220°-sin2(20°+30°)+sin20°cos(20°+30°)=-
| 1 |
| 4 |
sin230°-sin2(30°+30°)+sin30°cos(30°+30°)=-
| 1 |
| 4 |
∴猜想出一个反映一般规律的等式:sin2θ-sin2(θ+30°)+sinθcos(θ+30°)=-
| 1 |
| 4 |
故答案为:sin2θ-sin2(θ+30°)+sinθcos(θ+30°)=-
| 1 |
| 4 |
点评:探索规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律.揭示的规律,常常包含着事物的序列号.所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘.掌握探究的一般方法是解决此类问题的关键.

练习册系列答案
相关题目
若集合M={-1,0,1,2},N={1,0},则M∪N=( )
| A、{0,1} |
| B、{-1,0,1,2} |
| C、{-1,0,1} |
| D、{0,1,2} |
函数y=x3-2x2+2x共有( )个极值.
| A、0 | B、1 | C、2 | D、3 |
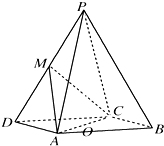 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ADC=60°,AD=AM=1,PC=2,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ADC=60°,AD=AM=1,PC=2,M为PD的中点.