题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() 。
。
(1)证明:![]() ,并求
,并求![]() 的通项公式;
的通项公式;
(2)构造数列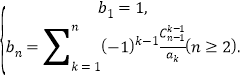 求证:无论给定多么大的正整数
求证:无论给定多么大的正整数![]() ,都必定存在一个
,都必定存在一个![]() ,使
,使![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由![]() 及
及![]() ,得
,得![]() 。由
。由![]() ,
,![]() 及
及![]() ,得
,得![]() 。
。
下面用数学归纳法证明:![]() ,即
,即![]()
![]() .①
.①
(i)当![]() 时,由
时,由![]() ,
,![]() ,知①成立。
,知①成立。
(ii)假设![]() 时,①成立,即
时,①成立,即![]() ,
,![]() ,有
,有![]() ,约去
,约去![]() 得
得![]() .移项并代入
.移项并代入![]() 得
得![]()
![]()
![]() .②则
.②则![]()
![]() 。
。
约去![]() 得
得![]() .约去
.约去![]() 得
得![]() ,
,
移项并代入![]() 得
得![]() .②由式②、③知,当
.②由式②、③知,当![]() 时,①成立,综上得证式①成立。
时,①成立,综上得证式①成立。
合并得![]() ,这就证明了
,这就证明了![]() ,且求出了通项
,且求出了通项![]() 。
。
(2)把![]() 代入,对
代入,对![]() 有
有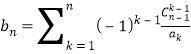
![]()
![]()
![]()
![]()
![]() 。
。
因为![]()
![]() ,
,
所以,对于给定的正整数![]() ,存在一个
,存在一个![]() ,使
,使![]()
![]()
![]()
![]() 。
。
说明:第(1)问用公式![]() 可得
可得![]()
![]() ,
,
但需![]() ,才能推出
,才能推出![]() ,
,
此解法特点是“证明![]() ,并求
,并求![]() 的通项公式”同时进行。
的通项公式”同时进行。
第(2)问的一个背景是调和级数![]() 发散,证明不是唯一的。
发散,证明不是唯一的。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目