题目内容
【题目】我们把一系列向量![]() 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作![]() .已知向量列
.已知向量列![]() 满足
满足![]() 且
且![]() .
.
(1)证明数列![]() 是等比数列;
是等比数列;
(2)求![]() 间的夹角
间的夹角![]() ;
;
(3)设![]() ,问数列
,问数列![]() 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
【答案】(1)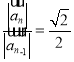 ;(2)
;(2)![]() ;(3)存在,最小项为
;(3)存在,最小项为![]()
【解析】
(1)通过向量模的定义计算即可证明;
(2)由数量积的定义求解即可;
(3)通过假设数列![]() 中的第
中的第![]() 项最小,找出数列的单调性计算即可
项最小,找出数列的单调性计算即可
(1)证明:根据题意,
得![]() ,
,
当![]() 时,
时,![]()
所以,数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列
(2)由(1)可得,
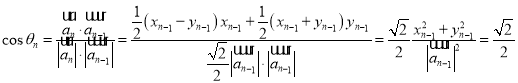 ,
,
所以![]()
(3)数列![]() 中存在最小项,
中存在最小项,
由(1)可得, 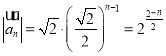 ,
,
所以![]() ,
,
假设![]() 中的第
中的第![]() 项最小,由
项最小,由![]() ,
,![]() ,
,
所以![]() ,
,
当![]() 时,有
时,有![]() ,由
,由![]() 得
得![]() ,
,
即![]() ,则
,则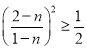 ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() 时,即有
时,即有![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,
,
所以![]()
故数列![]() 中存在最小项,最小项是
中存在最小项,最小项是![]()

练习册系列答案
相关题目