题目内容
【题目】已知直线![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和点
和点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求定点![]() 的坐标与圆
的坐标与圆![]() 的方程;
的方程;
(2)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点![]() ,问:在
,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)存在,
;(2)存在,![]() 或
或![]() .
.
【解析】
(1)可采用分离参数法求出直线恒过的定点![]() ,设圆
,设圆![]() 的方程为
的方程为![]() ,将
,将![]() 两点代入一般方程,又圆心
两点代入一般方程,又圆心![]() 过直线,故有
过直线,故有![]() ,联立求解即可;
,联立求解即可;
(2)由![]() 为直径对应的两个端点,根据对称关系先求得点
为直径对应的两个端点,根据对称关系先求得点![]() ,可判断点
,可判断点![]() 在圆外,故直角存在两种情况,以点
在圆外,故直角存在两种情况,以点![]() 为直角和以点
为直角和以点![]() 为直角,结合两直线垂直斜率之积为-1即可求得点
为直角,结合两直线垂直斜率之积为-1即可求得点![]()
(1)由![]() 得,
得,![]() ,
,
令![]() ,得
,得![]() ,即定点
,即定点![]() 的坐标为
的坐标为![]() .
.
设圆![]() 的方程为
的方程为![]() ,
,
由条件得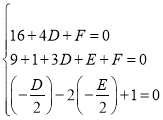 ,解得
,解得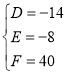 .
.
所以圆![]() 的方程为
的方程为![]() .
.
(2)圆![]() 的标准方程为
的标准方程为![]() ,
,![]() ,设点
,设点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,则有
,则有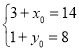 ,解得
,解得![]() ,
,![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .因为
.因为![]() 在圆外,所以点
在圆外,所以点![]() 不能作为直角三角形的顶点,
不能作为直角三角形的顶点,
若点![]() 为直角三角形的顶点,则有
为直角三角形的顶点,则有![]() ,
,
若点![]() 是直角三角形的顶点,则有
是直角三角形的顶点,则有![]() ,
,
综上,![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望
附:![]() ,
,
| 0.05 | 0.01 |
| 3.841 | 6.635 |