题目内容
(1)设椭圆 +
+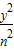 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,求椭圆的标准方程.
,求椭圆的标准方程.(2)设双曲线与椭圆
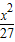 +
+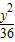 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.
【答案】分析:(1)由抛物线方程得到它的焦点坐标为F(2,0)也是椭圆的右焦点,由此得到m2-n2=4.根据椭圆离心率为 ,得到m2-n2=
,得到m2-n2= m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;
m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;
(2)根据椭圆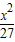 +
+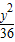 =1经过点A的纵坐标为4,算出A的横坐标是
=1经过点A的纵坐标为4,算出A的横坐标是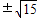 ,得A(
,得A(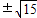 ,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为
,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为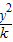 -
-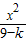 =1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.
=1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.
解答:解:(1)∵抛物线y2=8x的焦点坐标为F(2,0)
∴椭圆 +
+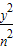 =1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…①
=1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…①
∵椭圆的离心率e=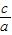 =
= ,∴
,∴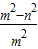 =
= …②
…②
联解①②,得m2=16,n2=12
∴该椭圆的标准方程为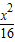 +
+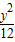 =1;
=1;
(2)∵椭圆 +
+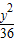 =1经过点A的纵坐标为4
=1经过点A的纵坐标为4
∴设A(t,4),可得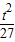 +
+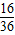 =1,解之得t=
=1,解之得t=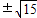 ,A(
,A(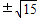 ,4)
,4)
∵椭圆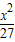 +
+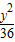 =1的焦点为(0,±3),双曲线与椭圆
=1的焦点为(0,±3),双曲线与椭圆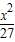 +
+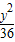 =1有相同的焦点,
=1有相同的焦点,
∴双曲线的焦点为(0,±3),因此设双曲线方程为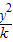 -
-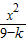 =1(0<k<9)
=1(0<k<9)
将点A( ,4)代入,得
,4)代入,得 -
-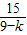 =1,解之得k=4(舍负)
=1,解之得k=4(舍负)
∴双曲线方程为 =1
=1
点评:本题给出两个曲线有公共的焦点,在已知它们一个交点坐标的情况下求曲线的方程,着重考查了椭圆、双曲线和抛物线的标准方程和简单几何性质等知识,属于基础题.
 ,得到m2-n2=
,得到m2-n2= m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;
m2,联解得到m2=16,n2=12,即得该椭圆的标准方程;(2)根据椭圆
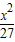 +
+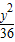 =1经过点A的纵坐标为4,算出A的横坐标是
=1经过点A的纵坐标为4,算出A的横坐标是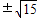 ,得A(
,得A(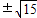 ,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为
,4).算出椭圆的焦点坐标为(0,±3)也是双曲线的焦点,由此可设双曲线方程为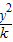 -
-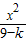 =1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.
=1(0<k<9),代入点A坐标解出k=4,从而得到此双曲线的标准方程.解答:解:(1)∵抛物线y2=8x的焦点坐标为F(2,0)
∴椭圆
 +
+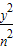 =1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…①
=1(m>0,n>0)的右焦点为F(2,0),可得m2-n2=4…①∵椭圆的离心率e=
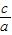 =
= ,∴
,∴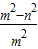 =
= …②
…②联解①②,得m2=16,n2=12
∴该椭圆的标准方程为
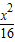 +
+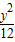 =1;
=1;(2)∵椭圆
 +
+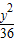 =1经过点A的纵坐标为4
=1经过点A的纵坐标为4∴设A(t,4),可得
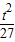 +
+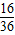 =1,解之得t=
=1,解之得t=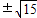 ,A(
,A(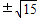 ,4)
,4)∵椭圆
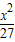 +
+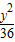 =1的焦点为(0,±3),双曲线与椭圆
=1的焦点为(0,±3),双曲线与椭圆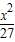 +
+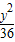 =1有相同的焦点,
=1有相同的焦点,∴双曲线的焦点为(0,±3),因此设双曲线方程为
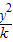 -
-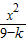 =1(0<k<9)
=1(0<k<9)将点A(
 ,4)代入,得
,4)代入,得 -
-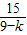 =1,解之得k=4(舍负)
=1,解之得k=4(舍负)∴双曲线方程为
 =1
=1点评:本题给出两个曲线有公共的焦点,在已知它们一个交点坐标的情况下求曲线的方程,着重考查了椭圆、双曲线和抛物线的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 已知椭圆C:
已知椭圆C:






