Question

已知椭圆C₁：

x2

5

+

y2

2

=1和圆C：x²+y²=4，且圆C与x轴交于A₁，A₂两点．
（1）设椭圆C₁的右焦点为F，点P的圆C上异于A₁，A₂的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明；
（2）设点M（x₀，y₀）在直线x+y-3=0上，若存在点N∈C，使得∠OMN=60°（O为坐标原点），求x₀的取值范围．

Answer 1

分析：（1）根据椭圆方程可求得焦点坐标和右准线方程，设点P，代入圆方程求得x₀，y₀的关系，进而表示出直线PF，OQ的斜率，进而可推断出直线OQ的方程，把x=2

2

代入求得y，求得Q点的坐标，进而求得PQ的斜率的表达式，结果与OP的斜率乘积为-1，推断出OP⊥PQ进而可知直线P与圆C相切
（2）设∠OMN=θ，则依题意可知θ≥60°，进而求得sinθ的范围，根据ON=2确定OM的范围，进而根据点M在直线l上，求得x₀，y₀的关系式，进而根据x₀²+y₀²≤

16

3

，求得x₀的取值范围．

解答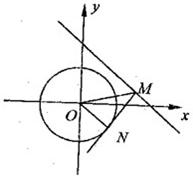：解：（1）直线P与圆C相切．
证明如下：易得椭圆C₁的右焦点为F（

2

，0），
右准线为x=2

2

设点P（x₀，y₀）则有x₀²+y₀²=4，
又k_PF=

y0

x0- 2

，k_OQ=-

x0- 2

y0

∴直线OQ的方程为y=

x0- 2

y0

x
令x=2

2

，得y=-

2 2 (x0- 2 )

y0

，
即Q（2

2

，-

2 2 (x0- 2 )

y0

）
∴k_PQ=

y0+ 2 2 (x0- 2 ) y0

x0-2 2

=-

x0(x0-2 2 )

y0(x0-2 2)

=-

x0

y0

又k_OP=

y0

x0

于是有k_PQ•k_OP=-1，故OP⊥PQ，直线P与圆C相切
（2）如图，设∠OMN=θ，则θ≥60°，
即sinθ≥

3

2

，即

ON

OM

≥

3

2

，
而ON=2，∴OM≤

4

3

∵M（x₀，y₀），∴x₀²+y₀²≤

16

3

，
又由M（x₀，y₀）∈l，得x₀+y₀=3，
∴y₀=3-x₀，于是有x₀²+（3-x₀）²≤

16

3

，
整理，得6x₀²-18x₀+11≤0，
解得

9- 15

6

≤x₀≤

9+ 15

6

∴x₀的取值范围是[

9- 15

6

，

9+ 15

6

]

点评：本题主要考查了直线与圆锥曲线的综合问题．直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容，问题的解决具有入口宽、方法灵活多样等，而不同的解题途径其运算量繁简差别很大，故此类问题能有效地考查考生分析问题、解决问题的能力，故应作为平时复习的重点．