题目内容
已知圆C:![]() ,直线
,直线![]() ,
,
(1) 无论m取任何实数,直线![]() 必经过一个定点,求出这个定点P的坐标。
必经过一个定点,求出这个定点P的坐标。
(2) 当m取任意实数时,试判断直线![]() 和圆的位置关系,并说明理由。
和圆的位置关系,并说明理由。
(3) 请判断直线![]() 被圆C截得的弦何时最短,并求截得的弦最短时m的值以及弦的长度
被圆C截得的弦何时最短,并求截得的弦最短时m的值以及弦的长度![]() 。
。
(1) 直线:![]()
![]() 可变形
可变形![]()
 。因此直线
。因此直线![]() 恒过定点P(-2,2)
恒过定点P(-2,2)
(2) 因为已知圆的圆心C(1,3),半径r=4,而![]() ,
,
所以直线![]() 过圆C
过圆C![]() 内一定点
内一定点![]() ,
,
故不论m取何值,直线![]() 和圆总相交。
和圆总相交。
(3)当直线![]() 垂直于CP时,截得的弦最短,此时,
垂直于CP时,截得的弦最短,此时,![]()
![]() ,
, ![]() ,得
,得![]() .
.
∴ 最短弦长为![]() 所以
所以![]() ,
, ![]()

练习册系列答案
相关题目
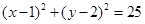 ,直线L:
,直线L: 

 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点; ,直线
,直线 :mx-y+1-m=0
:mx-y+1-m=0 =3
=3 ,求直线
,求直线