题目内容
(本小题满分12分)已知圆C: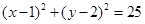 ,直线L:
,直线L: 

(1) 证明:无论 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2) 求直线被圆C截得的弦长最小时直线L的斜截式方程.
(1)见解析;(2)y=2x-5.
解析试题分析:(1)将L的方程整理为(x+y-4)+m(2x+y-7)=0
由 得
得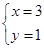 ∴直线L经过定点A(3,1)
∴直线L经过定点A(3,1)
∵(3-1)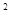 +(1-2)
+(1-2)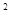 =5<25 ∴点A在圆C的内部,故直线L与圆恒有两个交点
=5<25 ∴点A在圆C的内部,故直线L与圆恒有两个交点
(2)圆心M(1,2),当截得弦长最小时,则L⊥AM,由k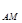 =
= 得
得
L的方程为y-1=2(x-3) ,即y=2x-5.
考点:直线系方程;直线与圆的位置关系;直线的斜截式方程。
点评:熟练求出直线系方程所过定点是解本题的关键。
(1)平行直线系:与Ax+By+C=0平行的直线为:Ax+By+C1=0(C1≠C)。
(2)垂直直线系:与Ax+By+C=0垂直的直线为:Bx-Ay+C1=0。
(3)定点直线系:若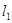 :
: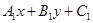 =0和
=0和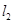 :
: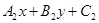 =0相交,则过
=0相交,则过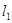 与
与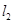 交点的直线系为
交点的直线系为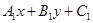 +λ(
+λ(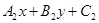 )=0。
)=0。

练习册系列答案
相关题目