题目内容
椭圆
+
=1（x≥0，y≥0）与直线x-y-5=0的距离的最小值为 ．
| x2 |
| 9 |
| y2 |
| 4 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：画出椭圆的图形以及直线的方程，找出曲线上的点与直线x-y-5=0的距离的最小值，即可利用点到直线的距离个数求解点P到直线x-y-5=0的距离最小值．
解答：
解：在坐标系中画出椭圆
+
=1（x≥0，y≥0）与直线x-y-5=0的图形，如图：可知（3，0）到直线x-y+5=0的距离最小，d=
=
．
故答案为：
．
解：在坐标系中画出椭圆| x2 |
| 9 |
| y2 |
| 4 |
| |3-5| | ||
|
| 2 |
故答案为：
| 2 |
点评：本题考查直线与椭圆的位置关系，解题的关键是利用数形结合找出点的位置，考查点到直线的距离公式的应用．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
已知向量
={3，4}，
•
=5，|
-
|=2
，则|
|=（ ）
| b |
| a |
| b |
| a |
| b |
| 5 |
| a |
| A、5 | ||
| B、25 | ||
C、2
| ||
D、
|
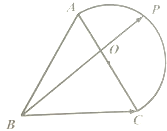已知△ABC是边长为2的正三角形，以AC为直径作半圆O（如图），P为半圆上任一点，则