题目内容
数列{an} (n∈N*)为递减的等比数列,且a1和a3为方程logm(5x﹣4x2)=0(m>0且m≠1)的两个根.
(1)求数列{an}的通项公式;
(2)记bn=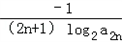 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)记bn=
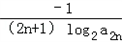 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.解:(1)方程logm(5x-4x2)=0(m>0且m≠1)即 5x﹣4x2=1,即4x2﹣5x+1=0.
利用韦达定理可得a1 +a3= ,a1 a3=
,a1 a3= .
.
再由数列{an} (n∈N*)为递减的等比数列
可得a1 =1,a3= ,
,
故公比为 .
.
∴an=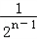 .
.
(2)∵bn=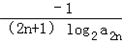 =
=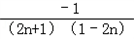
=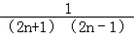 =
= (
(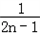 ﹣
﹣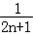 ).
).
∴数列{bn}的前n项和
Sn= [(1﹣
[(1﹣ )+
)+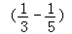 +
+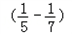 +…+
+…+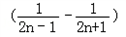 =
= (1﹣
(1﹣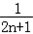 )=
)=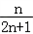 .
.
利用韦达定理可得a1 +a3=
 ,a1 a3=
,a1 a3= .
.再由数列{an} (n∈N*)为递减的等比数列
可得a1 =1,a3=
 ,
,故公比为
 .
.∴an=
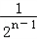 .
.(2)∵bn=
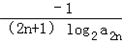 =
=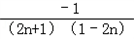
=
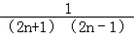 =
= (
(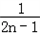 ﹣
﹣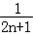 ).
).∴数列{bn}的前n项和
Sn=
 [(1﹣
[(1﹣ )+
)+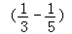 +
+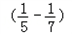 +…+
+…+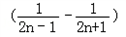 =
= (1﹣
(1﹣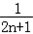 )=
)=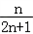 .
.
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目