题目内容
已知椭圆两焦点坐标分别是F1(0,-2),F2(0,2),并且经过点 ,求椭圆的标准方程.
,求椭圆的标准方程.
解:依题意,设所求椭圆方程为 …(2分)
…(2分)
因为点 在椭圆上,又c=2,得
在椭圆上,又c=2,得 …(8分)
…(8分)
解得 …(10分)
…(10分)
故所求的椭圆方程是 …(12分)
…(12分)
分析:设出椭圆的标准方程,代入点的坐标,即可求得椭圆的标准方程.
点评:本题考查椭圆的标准方程,考查学生的计算能力,属于基础题.
 …(2分)
…(2分)因为点
 在椭圆上,又c=2,得
在椭圆上,又c=2,得 …(8分)
…(8分)解得
 …(10分)
…(10分)故所求的椭圆方程是
 …(12分)
…(12分)分析:设出椭圆的标准方程,代入点的坐标,即可求得椭圆的标准方程.
点评:本题考查椭圆的标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
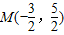 ,求椭圆的标准方程.
,求椭圆的标准方程.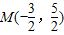 ,求椭圆的标准方程.
,求椭圆的标准方程.