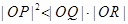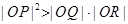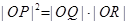题目内容
设双曲线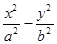 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
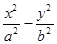 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为A.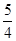 | B.5 | C.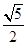 | D.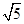 |
D
试题分析:双曲线
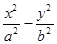 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,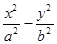 =1的渐近线方程为
=1的渐近线方程为 ,不妨将
,不妨将 代入y=x2+1整理得, x2-
代入y=x2+1整理得, x2- +1=0,由
+1=0,由 =
=  得,
得, =4,
=4, ,故选D。
,故选D。点评:典型题,涉及圆锥曲线的几何性质问题,往往涉及a,b,c,e的关系,应熟记。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 的一条渐近线为
的一条渐近线为 ,且右焦点与抛物线
,且右焦点与抛物线
 的焦点重合,则常数
的焦点重合,则常数 的值为 ( )
的值为 ( )



 ,焦点到渐近线的距离为3,则该双曲线的方程为______
,焦点到渐近线的距离为3,则该双曲线的方程为______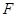 是双曲线
是双曲线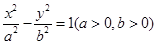 的左焦点,
的左焦点,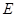 是双曲线的右顶点,过点
是双曲线的右顶点,过点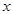 轴的直线与双曲线交于
轴的直线与双曲线交于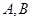 两点,若
两点,若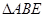 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率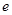 的取值范围为( )
的取值范围为( )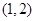
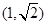
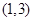
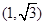
 的焦点为
的焦点为 ,则该双曲线的渐近线方程是( )
,则该双曲线的渐近线方程是( )



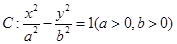 的离心率
的离心率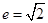 且点
且点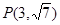 在双曲线C上.
在双曲线C上. 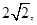 求直线l的方程.
求直线l的方程. 
 的两个焦点为
的两个焦点为 、
、 ,双曲线上一点
,双曲线上一点 到
到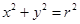 上任意一点
上任意一点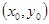 处的切线方程为:
处的切线方程为: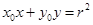 。类比以上结论有:双曲线:
。类比以上结论有:双曲线: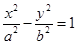 上任意一点
上任意一点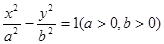 的右顶点为
的右顶点为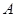 ,
,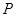 为双曲线上的一个动点(不是顶点),从点
为双曲线上的一个动点(不是顶点),从点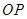 分别交于
分别交于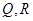 两点,其中
两点,其中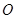 为坐标原点,则
为坐标原点,则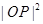 与
与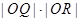 的大小关系为( )
的大小关系为( )