题目内容
18.已知x>0,y>0,若2y2+8x2-(m2-2m)xy>0恒成立,则实数m的取值范围是( )| A. | -2<m<4 | B. | -4<m<2 | C. | 2<m<4 | D. | -4<m<4 |
分析 将不等式2y2+8x2-(m2-2m)xy>0恒成立转化为m2-2m<($\frac{2y}{x}$+$\frac{8x}{y}$)min,利用基本不等式可求得($\frac{2y}{x}$+$\frac{8x}{y}$)min,再解不等式m2-2m<8即可得到答案.
解答 解:2y2+8x2-(m2-2m)xy>0恒成立?m2-2m<$\frac{{2y}^{2}+{8x}^{2}}{xy}$=$\frac{2y}{x}$+$\frac{8x}{y}$恒成立?m2-2m<($\frac{2y}{x}$+$\frac{8x}{y}$)min,
x>0,y>0,$\frac{2y}{x}$+$\frac{8x}{y}$≥2$\sqrt{\frac{2y}{x}•\frac{8x}{y}}$=8(当且仅当y=2x时取等号),
即($\frac{2y}{x}$+$\frac{8x}{y}$)min=8,
所以,m2-2m<8,
解得:-2<m<4,
故选:A.
点评 本题考查函数恒成立问题,分离参数是关键,考查等价转化思想与基本不等式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列函数在其定义域内即是奇函数又是单调递增函数的是( )
| A. | y=-$\frac{1}{x}$ | B. | y=-log2x | C. | y=3x | D. | y=x3 |
13.函数y=3sin(2x-$\frac{π}{3}$)的图象,可看作是把函数y=3sin2x的图象作以下哪个平移得到( )
| A. | 向左平移$\frac{π}{3}$ | B. | 向右平移$\frac{π}{3}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
3.sin480°的值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |

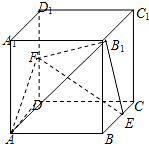 棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.
棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.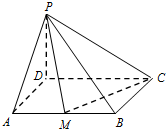 如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.
如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.