题目内容
（本小题满分12分）如图所示，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，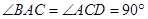
，AE∥C
D，DC=AC=2AE=2.
（Ⅰ）求证：平面BCD
平面ABC
（Ⅱ）求证：AF∥平面BDE；
（Ⅲ）求四面体B-CDE的体积.
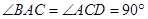，AE∥CD，DC=AC=2AE=2.（Ⅰ）求证：平面BCD
平面ABC（Ⅱ）求证：AF∥平面BDE；
（Ⅲ）求四面体B-CDE的体积.
（本小题满分12分）
解：（Ⅰ）∵面ABC面ACDE，面ABC
面ACDE=AC，CDAC，
∴DC面ABC，………………………………………………2分
又∵DC
面BCD，∴平面BCD平面ABC. ………………4分
（Ⅱ）取BD的中点P，连结EP、FP，则PF
DC,
又∵EADC，∴EAPF，……………………………6分
∴四边形AFPE是平行四边形，∴AF∥EP，
又∵EP面BDE，∴AF∥面BDE.…………………8分
（Ⅲ）∵BAAC，面ABC面ACDE=AC，∴BA面ACDE.
∴BA就是四面体B-CDE的高，且BA="2." ……………10分
∵DC=AC=2AE=2，AE∥CD，
∴
∴
∴
……………………………………12分
解：（Ⅰ）∵面ABC
面ACDE，面ABC面ACDE=AC，CDAC，∴DC
面ABC，………………………………………………2分又∵DC
面BCD，∴平面BCD平面ABC. ………………4分（Ⅱ）取BD的中点P，连结EP、FP，则PF
DC,又∵EA
DC，∴EAPF，……………………………6分∴四边形AFPE是平行四边形，∴AF∥EP，
又∵EP
面BDE，∴AF∥面BDE.…………………8分（Ⅲ）∵BA
AC，面ABC面ACDE=AC，∴BA面ACDE.∴BA就是四面体B-CDE的高，且BA="2." ……………10分
∵DC=AC=2AE=2，AE∥CD，
∴
∴
∴
……………………………………12分略
练习册系列答案
相关题目
三点的截面和球心的距离为球半径的一半，且
，则球的表面积为 
),则这个几何体的体积为（ ）
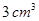
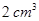
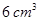
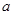平方米，且它的侧面展开图是一个半圆，则这个圆锥的底面的直径为__________________________
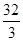π，则该正方体的表面积为（ ）
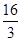
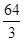
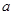的正方体外接球的表面积为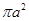
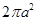
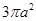
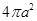
，则正方体的棱长等于_____________