题目内容
11．已知甲船在灯塔北偏东80°处，且与灯塔相距2km，乙船在灯塔北偏西40°处，两船相距3km，那么乙船与灯塔的距离为$\sqrt{6}$-1km．分析 由题意，画出示意图，先确定|AC|、|BC|和∠BAC的值，然后在△ABC中应用余弦定理可求得|AB|的值
解答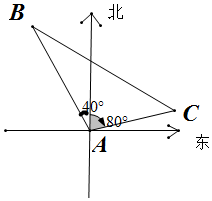 
解：由题意如图，可知|AC|=2，|BC|=3，∠BAC=120°，设BC=x，x＞0，
在△ABC中由余弦定理可得，
|BC|2=|AC|2+|AB|2-2|AC||AB|cos∠BAC得到9=4+x2-2×2×x•（-$\frac{1}{2}$），整理得x2+2x-5=0，解得x=$\sqrt{6}$-1；
∴|AB|=$\sqrt{6}$-1km．
故答案为：$\sqrt{6}-1$．
点评 本题主要考查余弦定理的应用，考查根据解三角形的有关定理来解决实际问题的能力．
练习册系列答案
相关题目
2．已知a+2b=1且b＞1，则$\frac{1}{a}$+$\frac{a}{b}$的取值范围（ ）
| A． | （-∞，1-2$\sqrt{2}$] | B． | （-2，1-2$\sqrt{2}$] | C． | [1-2$\sqrt{2}$，1+2$\sqrt{2}$] | D． | [1+2$\sqrt{2}$，4] |
3．定义在（0，$\frac{π}{2}$）上的函数f（x），f′（x）是它的导函数，且恒有f′（x）＜-f（x）tanx成立，则（ ）
| A． | $\sqrt{3}$f（$\frac{π}{3}$）＞f（$\frac{π}{6}$） | B． | $\sqrt{3}$f（$\frac{π}{3}$）＜f（$\frac{π}{6}$） | C． | $\frac{\sqrt{2}}{2}$f（1）＞cos1f（$\frac{π}{4}$） | D． | $\sqrt{2}$f（$\frac{π}{6}$）＜$\sqrt{3}$f（$\frac{π}{4}$） |
6．函数f（x）=sin2x+$\sqrt{3}$sinxcosx+1图象的一条对称轴方程为（ ）
| A． | x=$\frac{π}{2}$ | B． | x=$\frac{π}{3}$ | C． | x=$\frac{π}{4}$ | D． | x=$\frac{π}{6}$ |