题目内容
 (1)已知
(1)已知| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
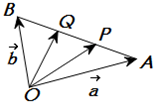
(2)如图,
| OA |
| a |
| OB |
| b |
①设点P,Q是线段AB的三等分点,试用
| a |
| b |
| OP |
| OQ |
②设点A1,A2,…,A2012是线段AB的2013等分点,试用
| a |
| b |
| OA1 |
| OA2 |
| OA2012 |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:(1)
与
为平行向量,存在实数λ,
=λ
,根据向量相等,建立关于λ,k的方程组求解.
(2)①利用向量加法法则,结合共线向量的性质求解.
②在①的基础上类比得出结果.
| a |
| b |
| b |
| a |
(2)①利用向量加法法则,结合共线向量的性质求解.
②在①的基础上类比得出结果.
解答:
解:(1)
与
为平行向量,存在实数λ,
=λ
,
∴k
+
=λ(2
-
)
∴k
+
=2λ
-λ
又
,
不共线
∴
∴k=-2.
(2)①
=
+
=
+
=
+
(
-
)=
+
,
即
=
+
同理
=
+
,
∴
+3
=
+
+
+2
=
+
,
②由①点P,Q是线段AB的三等分点时,
+
=
+
=
+
;
点A1,A2,…,A2012是线段AB的2013等分点时,
+
+…+
=(
+
)+(
+
)+…(
+
)=1006
+1006
.
| a |
| b |
| b |
| a |
∴k
| e1 |
| e2 |
| e1 |
| e2 |
∴k
| e1 |
| e2 |
| e1 |
| e2 |
又
| e1 |
| e2 |
∴
|
(2)①
| OP |
| OA |
| AP |
| OA |
| 1 |
| 3 |
| AB |
| a |
| 1 |
| 3 |
| b |
| a |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
即
| OP |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| OQ |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
∴
| OP |
| OQ |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| a |
| b |
| 5 |
| 3 |
| a |
| 7 |
| 3 |
| b |
②由①点P,Q是线段AB的三等分点时,
| OP |
| OQ |
| OA |
| OB |
| a |
| b |
点A1,A2,…,A2012是线段AB的2013等分点时,
| OA1 |
| OA2 |
| OA2012 |
| OA1 |
| OA2012 |
| OA2 |
| OA2012 |
| OA1006 |
| OA1007 |
| a |
| b |
点评:本题考查共线向量的性质,向量加法运算,类比猜想的思想方法.

练习册系列答案
相关题目
